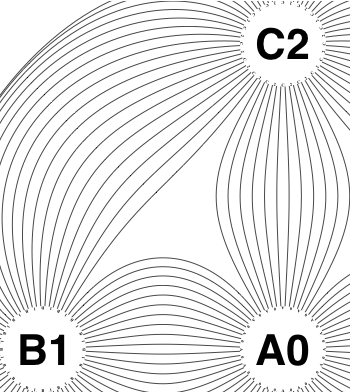
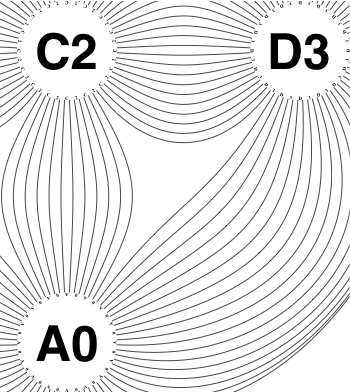
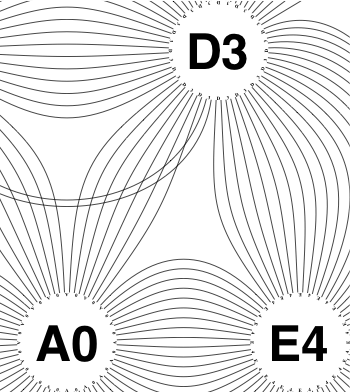
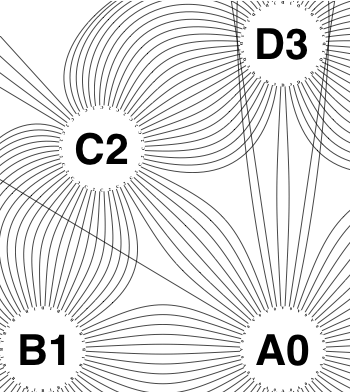
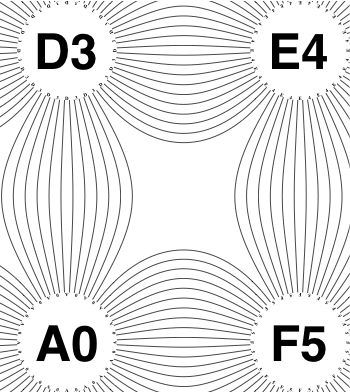
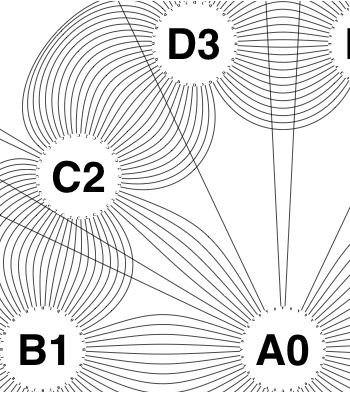
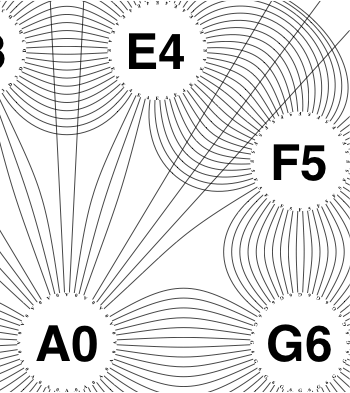
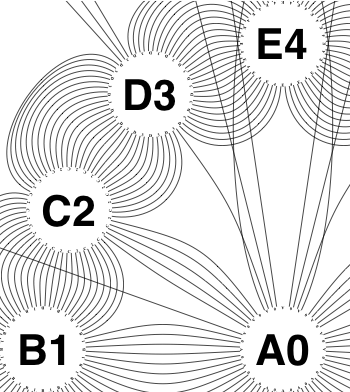
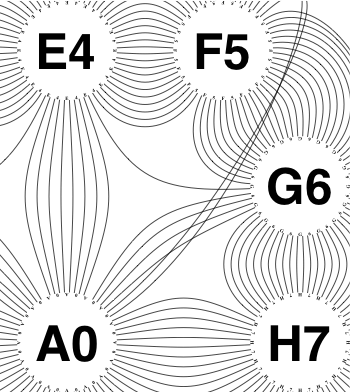
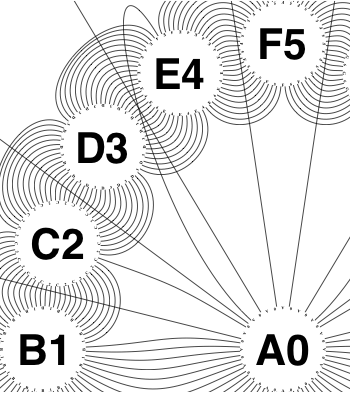
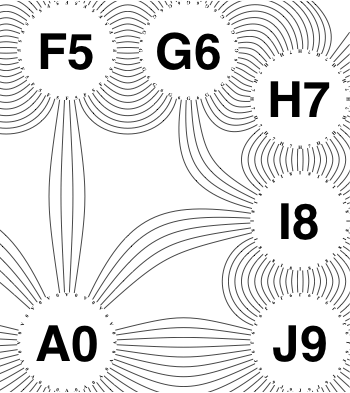
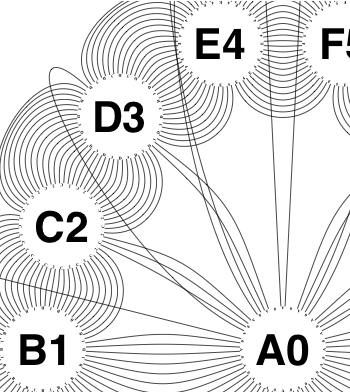
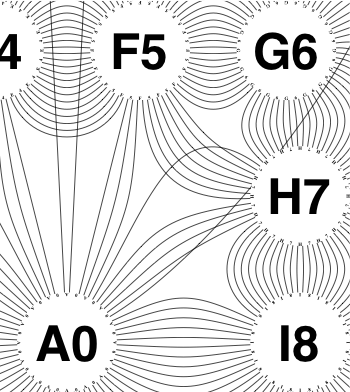
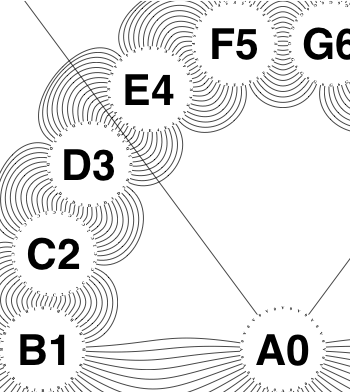
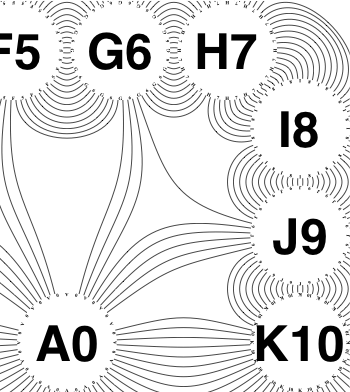
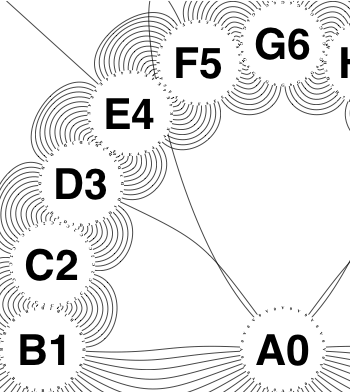
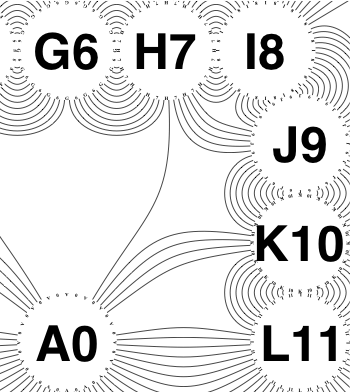
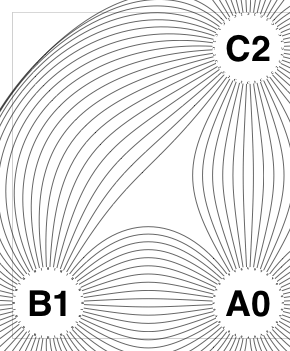
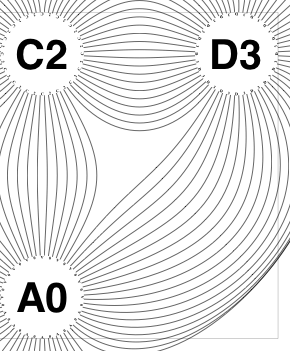
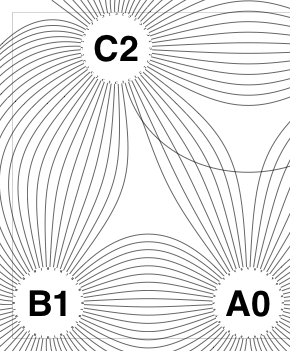
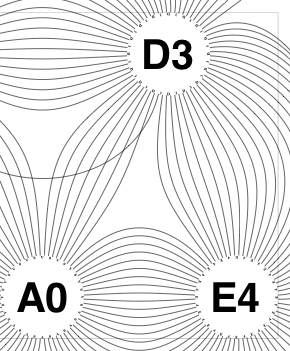
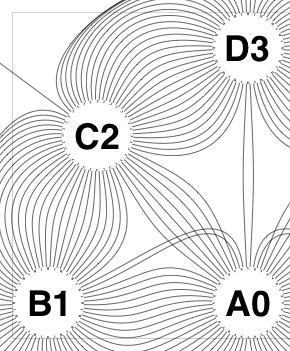
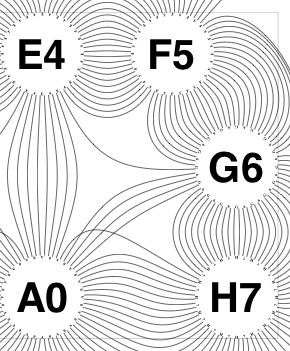
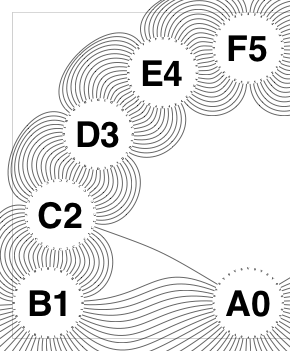
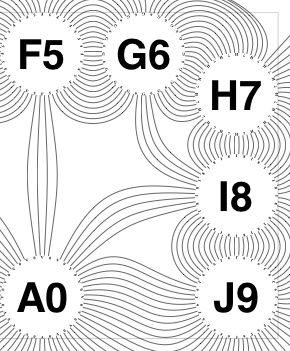
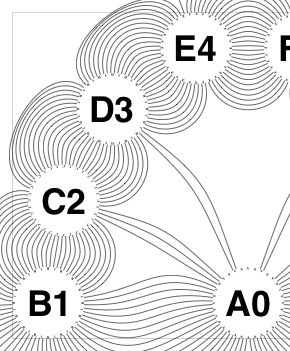
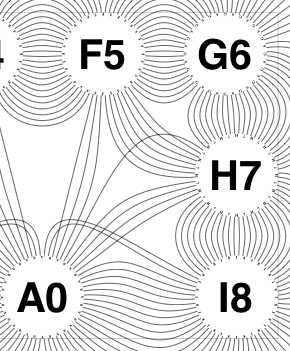
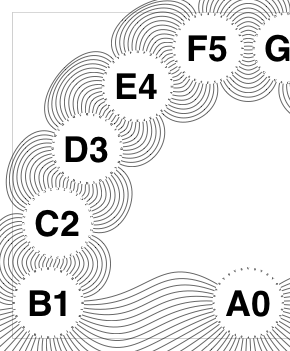
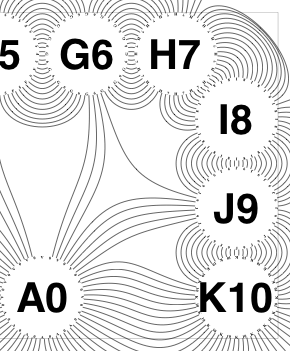
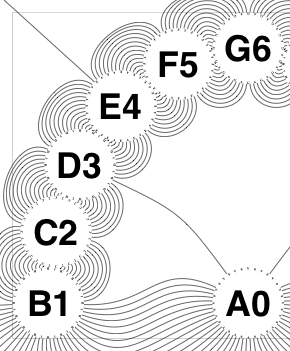
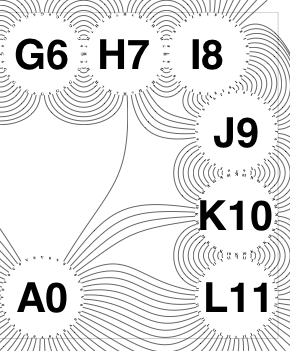
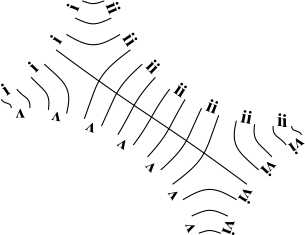
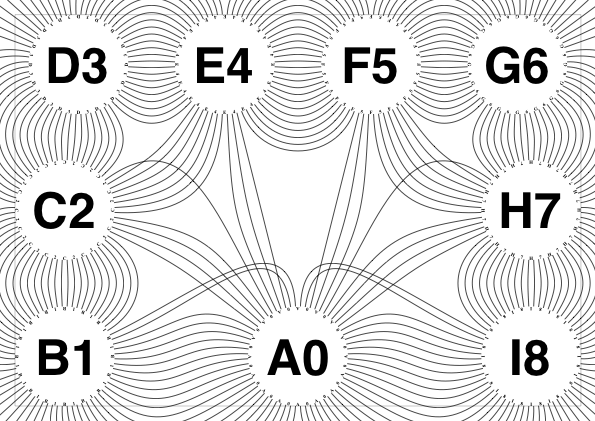
The new algorithm works as follows.
• Create an array of ends of rays, of length NumRayEnds. This array is to hold multiple fields, including X and Y (start point), dX and dY (start direction), Angle (also start direction), and the glass number from which originating. Another field is an array of distances to other ray ends, each of which is of length NumRayEnds.
• Populate the distances, being a task O(
n²). The definition of distance is slightly intricate. Compute the distance from start to start as the crow flies. The knot points will be half this crow distance from each end, of course in the direction implied by the relevant dX and dY. The ‘distance’ is deemed to be the sum of the distances between the knot points (the interesting bit of which is the central section, between the two interior know points).
• Create another field, sorted distances, pointing to the former array. (So for ray end
i, let the first element of the sorted array be
j, then the closest array end to
i is
j.)
• If
i is also the closest array end to
j, mark this pair as to be painted. (It probably will be painted.) Mark both
i and
j as painted, and repeat searching for new
i and
j that are the closest unpainted ends to each other.
• Repeat search till exhausted.
• It might be that
j is closed to
i,
k closest to
j, and
i closest to
k. So repeat the above, with a tolerance: if
j closest to
i, and
i within Tolerance of being closest to
j, repeat painting trick.
• Double tolerance, repeat. Repeat.
• Various
i-
j lines have been marked to be painted. That can still have intersections.
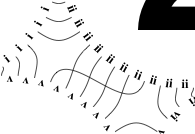
• So take all the lines connecting circles
ii and
v (WLOG). Compute the angles measured from the line connecting the centres of the circles; cut all the lines; separately sort the two lists of angles; re-connect. That detangles the two-circle problems.
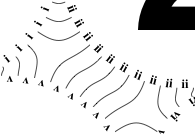
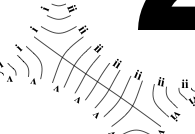
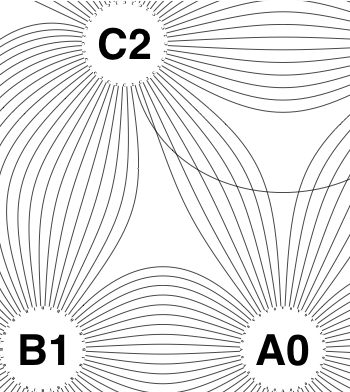
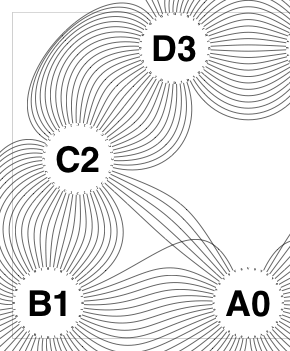
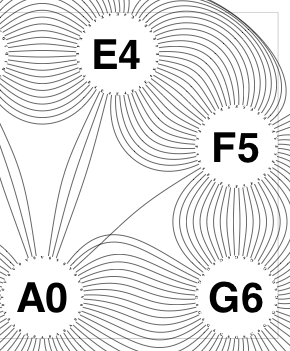
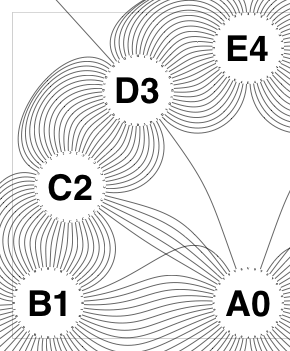
So the earlier problem of lines not intersecting has gone. And some of the tangled lines have been de-tangled particularly those of the form shown in the small counter-example above, repeated below.
jdaw1 wrote: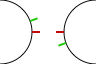
But that hasn’t eliminated all possible problems with tangling.