Software that makes placemats

[jdaw1]

∇v is the way to do it.

Let’s say both ∇ and ∇× (grad and curl) are known. What expression is the distance that may be travelled without turning by an angle of more than a°?

[akzy]

∇v is the way to do it.

Let’s say both ∇ and ∇× (grad and curl) are known. What expression is the distance that may be travelled without turning by an angle of more than a°?

Hmmm. No idea.
However, instead of a angle, you could just set a limit on the absolute value of the curl at that point - effectively the same thing right?

There might be a bit of confusion in the way that I suggested to evaluate so I shall try clarify (if you did understand it, then I've misunderstood something).At a point (x,y), we have a vector, v(x,y) which is pointing in a direction. I suggest that we follow that vector for a step size, h,

h=c / |∇v(x,y)|,

where c is a constant that we chose (be this a few millimeters or whatever works best).

If the field changes a lot in this region, then h will be small, if it changes very little, h will be larger. The vector is then evaluated at v(x+h_x,y+h_y) and the process is repeated.

[jdaw1]

h=c / |∇v(x,y)|,

where c is a constant that we chose (be this a few millimeters or whatever works best).

I suspect that curvature, or equivalently ∂angle/∂distance, are related to something like curl÷|grad|². Please help with the specific formal relationship.

[akzy]

The absolute curvature of a field is given by the eigenvectors of the hessian matrix (should give two for our case), where the hessian matrix is

hessian.PNG (19.79 KiB) Viewed 38916 times

phi_tot is the vector in our case (quick snatch and grab from my thesis)

This eigenvector can be evaluated spatially throughout the field. I suspect you are wanting the angle from the eigenvector. (I found these lecture slides which might help you get what you want, see pages 3 and 4 especially http://homepages.inf.ed.ac.uk/rbf/CVonl ... ffgeom.pdf)

[jdaw1]

Please inspect jdawiseman.com/2019/20190705_Droplets.pdf.

[akzy]

I like it.

I think you will need to make some exceptions for your starting seeds in the gaps between circles to take into account global and local symmetries. Each seed cannot sit on a line of symmetry and must instead sit slightly off (so then it has a definite direction to fly off in, and isn't confused by computational numerical errors).

[jdaw1]

Please inspect jdawiseman.com/2019/20190705_Droplets.pdf.

And jdawiseman.com/2019/20190706_Droplets.pdf.

[jdaw1]

I think you will need to make some exceptions for your starting seeds in the gaps between circles to take into account global and local symmetries. Each seed cannot sit on a line of symmetry and must instead sit slightly off (so then it has a definite direction to fly off in, and isn't confused by computational numerical errors).

Starting points are a triangular grid, rotated 15°, with moderate random offsets. From these are removed those outside margins. Paths are computed; and then removed are those ending outside the paintable box; and those ending very close to charges.

I think it’s good.

I propose to delete the Rays feature, which has never worked properly.

[jdaw1]

Providing your postscript code is fine with calculating potgrid analytically

It can.

How? More of a curiosity thing than anything. Differentiating analytically using a computer is something I never fully understood (I'm still convinced that wolfram works using magic). If you know of any good explanations (or fancy trying yourself) please send them my way.

Ahh, misunderstanding. I’ve done the differentiation, and have embedded that as a function which takes the charges and a point X,Y. Am not passing around and interpolating inside large 2d arrays of potentials.

[akzy]

Please inspect jdawiseman.com/2019/20190705_Droplets.pdf.

And jdawiseman.com/2019/20190706_Droplets.pdf.

This example looks really sharp. I think asymmetric charges will annoy some people to hell, but I think it looks great.

[jdaw1]

(I found these lecture slides which might help you get what you want, see pages 3 and 4 especially http://homepages.inf.ed.ac.uk/rbf/CVonl ... ffgeom.pdf)

I think not. It has curvature in a 3d sense. I want to know how fast the grad turns within the plane.

[jdaw1]

akzy: please check jdawiseman.com/2019/20190710_dAngle_dDistance.pdf. Thank you.

[jdaw1]

akzy: please check jdawiseman.com/2019/20190710_dAngle_dDistance.pdf. Thank you.

File updated to include cross terms (doh!).

[akzy]

akzy: please check jdawiseman.com/2019/20190710_dAngle_dDistance.pdf. Thank you.

File updated to include cross terms (doh!).

I presume that 'eps' is some step constant?

Apart from that, the methodology seems fine. I'm sure there's a slightly less winded way to do this. I had a play around with the hessian matrix and eigenvectors myself to no avail. I'm going to keep playing around with it and let you know if I have any success.

[jdaw1]

I presume that 'eps' is some step constant?

It’s epsilon, hence all the limiting to zero.

[jdaw1]

Done: example at jdawiseman.com/2019/20190711_Droplets.pdf.

[akzy]

Done: example at jdawiseman.com/2019/20190711_Droplets.pdf.

I'd be very pleased with a placemat like that. Well done indeed.

[jdaw1]

It didn’t print well. Some polishing of the output later, I’d welcome people test-printing, on A3, both
• 20190716_Droplets_t.pdf and
• 20190716_Droplets_f.pdf.

Please inspect smoothness of shape and greys of droplets. Which works? Which doesn’t? (Identify by different top-right headers: _f = two numbers; _t = two identical functions.)

Thank you.

Edit: and 20190718_Droplets.pdf.

[akzy]

Just printed them off now.

''f' comes out the worst for me. The leading edge of the drop is flat, and the tail is often broken.
't' and the edit version come out very similarly and at about 0.5m from the sheet, both stop looking pixelated. 't' comes out slightly edge for some droplets as it doesn't seem to create two hole in the droplet, which occurs in the edit version.

As a result, I think 't' looks the best.

[jdaw1]

Hence default droplet shape adjusted to that in 20190726_Droplets.pdf.

akzy: you made the original complaint. Please confirm resolved.

[akzy]

Hence default droplet shape adjusted to that in 20190726_Droplets.pdf.

akzy: you made the original complaint. Please confirm resolved.

It's a thumbs up from me.

[jdaw1]

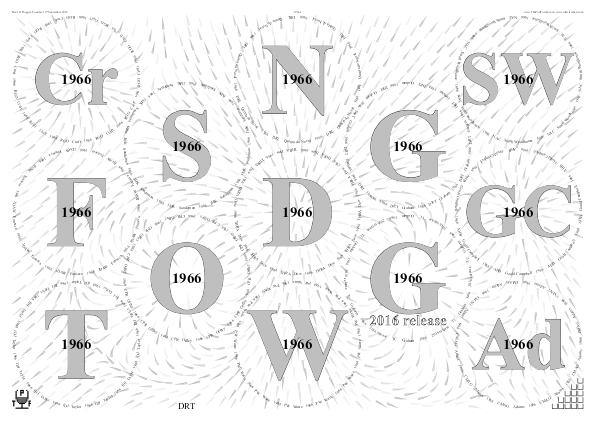
First use of droplets was at the 1966 horizontal on 10th Sept 2019 (placemats and parameters by which made).

In this DropletsCharges, there is a +20 attractive charge on Dow; -2 repelling charge on Offley; and other small charges not relevant for this calculation (+1 Cr; -3 G-2016); +1 GC). So going from Dow to a little past Offley, somewhere in Taylor’s circle, is a balance point (not quite Lagrange, nor quite a termination shock) which — for my palate — gives some intricate structure. Different opinions welcomed.

Where is this balance point? At a distance d past Offley, measured in radii, in Mathematica notation

Solve[{D[20/(d + 2)^2 - 2/d^2, d] == 0 && d > 0}, d]

That’s the real root of 9 d³ − 6 d² − 12 d − 8 = 0   ⇒   d ≈ 1.73, which is in happy optical agreement with the output.

[akzy]

I've never massively been a fan of these turning points, always caused me numerical nightmares. I'd be tempted to shift charges to hide it in the 'T' of Taylor's.

[jdaw1]

I've never massively been a fan of these turning points, always caused me numerical nightmares. I'd be tempted to shift charges to hide it in the 'T' of Taylor's.

But we’re doing different things. You are precisely modelling something difficult. Whereas I am using a simulation of a physical process to make something aesthetically appealing.

So I disagree.

[akzy]

I feel all the years of torment have had a terrible effect on me.

Where is this balance point? At a distance d past Offley, measured in radii, in Mathematica notation

Solve[{D[20/(d + 2)^2 - 2/d^2, d] == 0 && d > 0}, d]

That’s the real root of 9 d³ − 6 d² − 12 d − 8 = 0   ⇒   d ≈ 1.73, which is in happy optical agreement with the output.

Having a quick look at this, I notice that d~1.73~sqrt(3). Do you have any insight as to why this is the case?