But then you aren't a fan of Dow...djewesbury wrote:This does seem to make sense at first, but then picture yourself reaching for that first glass at the back of the mat.. It's something delicious, perhaps poured from a Fonseca 1970 mag that you'll be comparing with other formats.. Oh no, your sleeve has just caught the last glass - the Dow 1950! Oh well, it is a pretty colour on the placemat..Glenn E. wrote:putting a glass as close to the top left corner of the sheet is primary.
Software that makes placemats
- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Re: Software that makes placemats
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
There are pictures of all in the ‘Layout’ § of the manual.Glenn E. wrote:The remainder are likely attempts to be purely descriptive, but for me are just confusing.
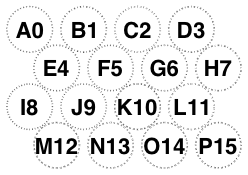
/Adjusted5 is like /Diamonds, but with the central circle adjusted towards a long edge, thereby making the circles a mite larger: 20090626, 20090626, 20090721, 20100805. So what it is doing is using the dead space around ‘C2’ in
 Â →
 → 
Re: Software that makes placemats
If we have oodles of table space each, such that 20+ glasses can be placed over multiple sheets of A3, I agree. But typically we don’t.djewesbury wrote:I always have a slight problem with very tightly-stacked placemats, which is that the first drink of the flight is the furthest away.. Perhaps this is why I'm pleased to see the new /Arch and /PostsAndLintel designs, which give clear access to every glass.
Re: Software that makes placemats
If it is easier for you, don’t stress about the rule. Instead, from each pair pick the one that is obviously definitely primary, or the one that is primary-ish, and also list the pairs about which you have little opinion. From which I can attempt to craft a rule.Glenn E. wrote:But the clarity fails when the other examples are perused. I need more time to ponder a solution, though my first impulse is to say that putting a glass as close to the top left corner of the sheet is primary.
Re: Software that makes placemats
We typically put the first glass to be consumed front left, so in theory I should prefer for front left to be primary. But those don't always look like primary to me either. I will attempt to find some commonality in my preferences.djewesbury wrote:This does seem to make sense at first, but then picture yourself reaching for that first glass at the back of the mat.. It's something delicious, perhaps poured from a Fonseca 1970 mag that you'll be comparing with other formats.. Oh no, your sleeve has just caught the last glass - the Dow 1950! Oh well, it is a pretty colour on the placemat..Glenn E. wrote:putting a glass as close to the top left corner of the sheet is primary.
Glenn Elliott
Re: Software that makes placemats
Upon further review, all of the sheets where bottom (or front) left is occupied either appear primary to me, or are of equal standing to their mirror. Therefore, the bottom left position being occupied can be called the primary sheet for me.jdaw1 wrote:If it is easier for you, don’t stress about the rule. Instead, from each pair pick the one that is obviously definitely primary, or the one that is primary-ish, and also list the pairs about which you have little opinion. From which I can attempt to craft a rule.Glenn E. wrote:But the clarity fails when the other examples are perused. I need more time to ponder a solution, though my first impulse is to say that putting a glass as close to the top left corner of the sheet is primary.
In fact, the ones that look odd either way are probably layouts that I wouldn't use anyway. I prefer to place 8 glasses in 3 rows, 3-2-3, for example. I would also simply place 3 glasses in a single row. So their default alignment in /Diamond is irrelevant to me.
Glenn Elliott
Re: Software that makes placemats
So you prefer to have front-left full, whereas my rule was to have front-right empty. As yet I’m not convinced that your rule is better. Please say more. Perhaps you could comment on the interaction with the water boxes, which are usually on the right.Glenn E. wrote:Therefore, the bottom left position being occupied can be called the primary sheet for me.
Our rules disagree when there are even numbers of rows and an odd number of columns, so for 3 and 14 glasses.
But agree otherwise:
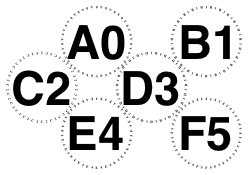
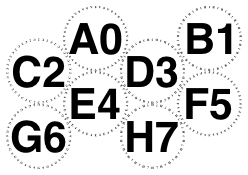
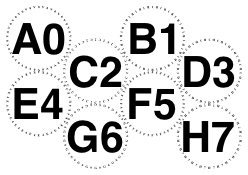
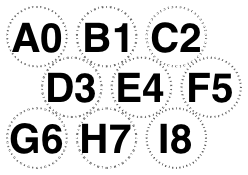
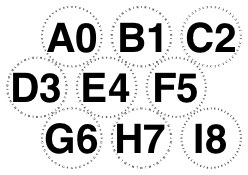
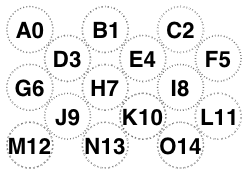
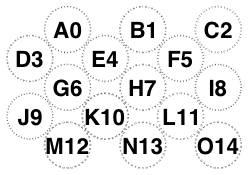
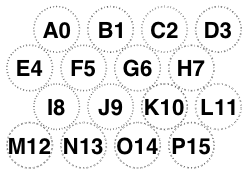
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
My preference would be for back-left-full to be primary.
Re: Software that makes placemats
We agree when rows+columns is odd:PhilW wrote:My preference would be for back-left-full to be primary.










We disagree when rows and columns are both even:








(And there is no question to answer when both are odd.)
I need some persuading of this rule. Please persuade.
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
For me, this is the natural way to look at a page. We read from top to bottom, left to right; The natural first place to look on a page is the top left; this is where I would expect the first glass to be.jdaw1 wrote:I need some persuading of this rule. Please persuade.PhilW wrote:My preference would be for back-left-full to be primary.
Re: Software that makes placemats
We have had three preferences, all different. I’m willing to be persuaded that mine is not the best, but so far I’m not.
Reminder: my preference is empty lower-right.
Reasoning in general
• Most people are right handed. So, for most people, the water boxes are on the lower right. It seems sensible to prefer a greater distance between that writing zone and the nearest glass.
• To pick up a glass in the upper-right triangle of the page, my right hand goes past this spot. Retreating that glass from that corner my help lessen the frequency of collisions.
Reasoning in particular


• Who can’t love a pretty smile?


For those accustomed to a left-to-right writing direction, the left-hand version appears to be ‘going forwards’; the other is going backwards.


• Same as four glasses: moving forwards, not backwards.


• No particular reasoning for eight glasses.


• Same as six glasses: moving forwards, not backwards.


• For fourteen the ‘particular’ reasoning might go the other way: does the right-hand version look more like a stable building, and the left look more rickety?


• Same as nine glasses (moving forwards, not backwards) but the effect is much diluted.


• No particular reasoning for sixteen glasses.
Reminder: my preference is empty lower-right.
Reasoning in general
• Most people are right handed. So, for most people, the water boxes are on the lower right. It seems sensible to prefer a greater distance between that writing zone and the nearest glass.
• To pick up a glass in the upper-right triangle of the page, my right hand goes past this spot. Retreating that glass from that corner my help lessen the frequency of collisions.
Reasoning in particular


• Who can’t love a pretty smile?


For those accustomed to a left-to-right writing direction, the left-hand version appears to be ‘going forwards’; the other is going backwards.


• Same as four glasses: moving forwards, not backwards.


• No particular reasoning for eight glasses.


• Same as six glasses: moving forwards, not backwards.


• For fourteen the ‘particular’ reasoning might go the other way: does the right-hand version look more like a stable building, and the left look more rickety?


• Same as nine glasses (moving forwards, not backwards) but the effect is much diluted.


• No particular reasoning for sixteen glasses.
- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Re: Software that makes placemats
left-to-rightjdaw1 wrote:
For those accustomed to a right-to-left writing direction, the left-hand version appears to be ‘going forwards’; the other is going backwards.
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
Fixed. Sorry.djewesbury wrote:left-to-right
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
Phenomenal D66 is currently saying you're wrong and I'm right, but I'm not convinced that's especially persuasive... might try something more coherent in the morning.jdaw1 wrote:We have had three preferences, all different. I’m willing to be persuaded that mine is not the best, but so far I’m not.
Re: Software that makes placemats
Is Dow 1966 a particularly argumentative Vintage Port? It is very excellent, so more likely to be right than any of us.PhilW wrote:Phenomenal D66 is currently saying you're wrong and I'm right
Re: Re: Software that makes placemats
For 3 glasses I agree that your rule is more aesthetically pleasing. But for 14 glasses I prefer the "weight" of the image at the bottom of the page.jdaw1 wrote:So you prefer to have front-left full, whereas my rule was to have front-right empty. As yet I’m not convinced that your rule is better. Please say more. Perhaps you could comment on the interaction with the water boxes, which are usually on the right.Glenn E. wrote:Therefore, the bottom left position being occupied can be called the primary sheet for me.
Our rules disagree when there are even numbers of rows and an odd number of columns, so for 3 and 14 glasses.



Since, as previously stated, I would probably not use /Diamond and would instead put 3 glasses in a single row, I don't really care about that case.
I don't have an issue with the water boxes, so that also doesn't affect my preference.
Avoiding collisions and the associated loss of Port, though, is sufficiently convincing. While I still find my rule more aesthetically pleasing for 14 glasses, aesthetics must yield to Port preservation.
Sent from my Galaxy Nexus using Tapatalk 2
Glenn Elliott
Re: Re: Software that makes placemats
jdaw1 wrote:• For fourteen the ‘particular’ reasoning might go the other way: does the right-hand version look more like a stable building, and the left look more rickety?
We agree. Sigh. That makes things complicated. Even if my preference isn’t strong.Glenn E. wrote:But for 14 glasses I prefer the "weight" of the image at the bottom of the page.
Maybe post-D66 PhilW can rescue us. Maybe.
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
I agree with you both on 14-glass case (preferring the weight at the bottom), though it's only a minor preference; I also would have no problem with this being the exception case for which we use a modifier (/Invert or similar) from the default.
The area I disagree is on the 4,6,8 cases (where really I am looking at the 4*N case, with 6 being a special case), where you describe preferring the ‘going forwards’ style; I do not - I strongly favour the one you refer to as 'going backwards'. To me, the left hand side of the page is the reference; it is where all unjustified text is referenced against, where the spine would be on the cover of a book, where the flagpole would be, etc. In the 4N case, the 'going backwards' variants seem to me to rest in a stable manner against this left side; like a stack leaning on a wall at the left, while the 'going forwards' style means that the stack, or odd bottles at the right would fall off.
The area I disagree is on the 4,6,8 cases (where really I am looking at the 4*N case, with 6 being a special case), where you describe preferring the ‘going forwards’ style; I do not - I strongly favour the one you refer to as 'going backwards'. To me, the left hand side of the page is the reference; it is where all unjustified text is referenced against, where the spine would be on the cover of a book, where the flagpole would be, etc. In the 4N case, the 'going backwards' variants seem to me to rest in a stable manner against this left side; like a stack leaning on a wall at the left, while the 'going forwards' style means that the stack, or odd bottles at the right would fall off.
Re: Software that makes placemats
Mrs W., who has just made a fabulous Welsh Rarebit, will be asked to adjudicate. Of course, ‘blind’, meaning that she won’t be told who prefers which.
And I’ll also make some /Portrait examples.
And I’ll also make some /Portrait examples.
Re: Software that makes placemats
/Portrait /Diamonds
The following examples of /Diamonds with orientation /Portrait has changed my preferred rule.
• If the number of rows is even and number of glasses ≥4, then bottom corners full.
• Otherwise old rule of bottom-right being empty.
In particular, six and nine and fifteen glasses need to point up. However, this still doesn’t agree with PhilW. Awaiting Mrs W.’s availability.
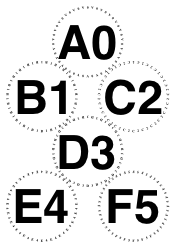
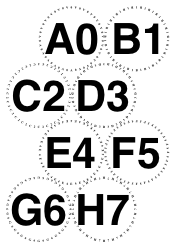
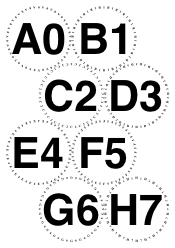
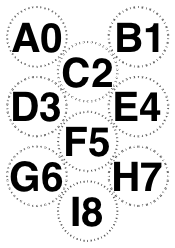

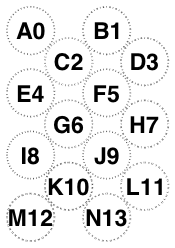

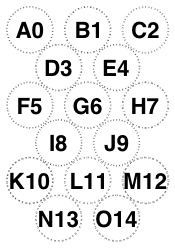
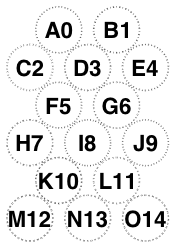

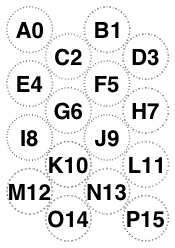
The following examples of /Diamonds with orientation /Portrait has changed my preferred rule.
• If the number of rows is even and number of glasses ≥4, then bottom corners full.
• Otherwise old rule of bottom-right being empty.
In particular, six and nine and fifteen glasses need to point up. However, this still doesn’t agree with PhilW. Awaiting Mrs W.’s availability.


















Re: Software that makes placemats
In all of these cases, my rule applies. Bottom-left full.jdaw1 wrote:/Portrait /Diamonds
The following examples of /Diamonds with orientation /Portrait has changed my preferred rule.
• If the number of rows is even and number of glasses ≥4, then bottom corners full.
• Otherwise old rule of bottom-right being empty.
Are there examples of /Portrait /Diamonds where bottom-left full does not provide agreement between us?
Glenn Elliott
Re: Software that makes placemats
Glenn E. wrote:Are there examples of /Portrait /Diamonds where bottom-left full does not provide agreement between us?
Only when glasses ≤ 3.jdaw1 wrote:and number of glasses ≥4
It’s a fair cop. I’ll come quietly.Glenn E. wrote:In all of these cases, my rule applies. Bottom-left full.
Re: Software that makes placemats
Decision taken and coded. Bottom-left full, unless there are exactly two rows and three columns.
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
grumble /mirror grumble. Though to be fair, your water boxes argument does.. er.. hold water.jdaw1 wrote:Decision taken and coded. Bottom-left full, unless there are exactly two rows and three columns.
Re: Software that makes placemats
• /Mirror, camel case.PhilW wrote:grumble /mirror grumble. Though to be fair, your water boxes argument does.. er.. hold water.jdaw1 wrote:Decision taken and coded. Bottom-left full, unless there are exactly two rows and three columns.
• Nobody had passionate views. Indeed, I asked because I didn’t. But I managed to change my mind, and Glenn observed thatI had changed it to match his. That was a majority.
But [ /Diamonds /Mirror ] is available to the dissenter.
Re: Software that makes placemats
Googling the problem of packing circles reveals much learned comment, and lists of best-known packings at Packomania.com. But, as posted in sci.math, the placemat software knows some to be better, most obviously that for 1607 circles on a square page. If using Bunghole-standard glasses, it would have to be a large page.
Re: Software that makes placemats
Very nice.
For smaller tastings, how about an A3 mat, guillotined lengthways (i.e 420 x 15mm), that can be placed near centre table (leaving uncluttered space for notes/meals etc.) and contain ports in an easy access row?
For smaller tastings, how about an A3 mat, guillotined lengthways (i.e 420 x 15mm), that can be placed near centre table (leaving uncluttered space for notes/meals etc.) and contain ports in an easy access row?
Rob C.
Re: Software that makes placemats
RAYC wrote:For smaller tastings, how about an A3 mat, guillotined lengthways (i.e 420 x 15mm), that can be placed near centre table (leaving uncluttered space for notes/meals etc.) and contain ports in an easy access row?
Might /BottomRow do the job?The manual wrote:There are also three simple designs, /TopRow, /MiddleRow, /BottomRow, each having everything in one row, with obvious vertical position. There is also /Sides, with the obvious meaning.
For more than a few glasses these are too cramped.
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
That would certainly leave the table uncluttered.RAYC wrote:(i.e 420 x 15mm)
Re: Software that makes placemats
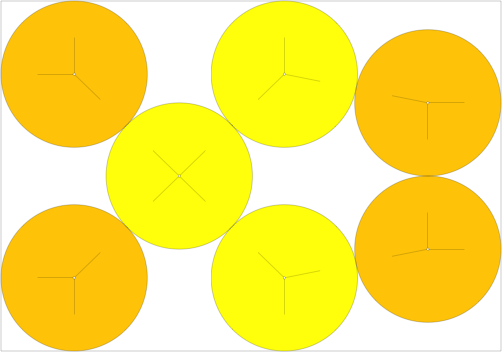
Packomania.com is for geeky mathematicians, and has lots of examples of packing circles of maximal radius in various containers, including 7×10 rectangles. That is close to the proportions of A4, less a fixed margin.
Observe Packomania’s best for for 7 circles and 10 on a 7×10 rectangle:
 Â
 
I’ll implement this as two on the right (/Landscape) or top (/Portrait), reversed for /Mirror, of course, and three-row (three-column) /Diamonds for the rest. Packomania’s 10-glass solution is an epsilon better than that, but generalising the asymmetry would be too complicated. Compared to plain seven-glass /Diamonds, that adds ≈5% to the radius. PW would have wanted that for Warre versus Fonseca tasting.
What should it be called?
Observe Packomania’s best for for 7 circles and 10 on a 7×10 rectangle:
 Â
 
I’ll implement this as two on the right (/Landscape) or top (/Portrait), reversed for /Mirror, of course, and three-row (three-column) /Diamonds for the rest. Packomania’s 10-glass solution is an epsilon better than that, but generalising the asymmetry would be too complicated. Compared to plain seven-glass /Diamonds, that adds ≈5% to the radius. PW would have wanted that for Warre versus Fonseca tasting.
What should it be called?
- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Software that makes placemats
Are you thinking architectural, prosaic, allusive..? I can't see anything in the pattern that would provide a short metaphorical name at present. I'm guessing it'll probably end up being something like /DiamondsPlusTwo or /DiamondsAsymmetricalSeven or something like that.
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
Current winner is ‟/DiamondsPlus”, which allows a little generalisation to something like Packomania’s 29-glass best:djewesbury wrote:/DiamondsPlusTwo

- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Software that makes placemats
I wouldn't like to be reaching for glass 16 on that placemat...
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
It’s printed on A0. Each glass can hold most of a bottle. By the time you reach glass 16, it would indeed be difficult.djewesbury wrote:I wouldn't like to be reaching for glass 16 on that placemat...
Re: Software that makes placemats
I can think of nothing better.jdaw1 wrote:Current winner is ‟/DiamondsPlus”
Glenn Elliott
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
Ditto. Some possible insect outlines came to mind, but ‟/DiamondsPlus” is probably simpler and clearer, and therefore preferred.Glenn E. wrote:I can think of nothing better.jdaw1 wrote:Current winner is ‟/DiamondsPlus”
- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Software that makes placemats
I quickly discarded /BeetleCarapacePhilW wrote:Ditto. Some possible insect outlines came to mind, but ‟/DiamondsPlus” is probably simpler and clearer, and therefore preferred.Glenn E. wrote:I can think of nothing better.jdaw1 wrote:Current winner is ‟/DiamondsPlus”
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
Step one: write code to solve a quartic equation. Worrying, I think that I have devised an algorithm as good as Brent’s Method, but simpler, and not needing a pre-chosen x-step.
Assume root bounded by LowerX and UpperX, with matching y values LowerY and UpperY. Interpolation would make the next x value be LowerX + (UpperX”“LowerX) × LowerY/(LowerY”“UpperY). This can fail for some shapes (e.g., y = x^4 ”“ c), as the interpolated value is always on the same side of the root, so only one side (say, LowerX) ever gets moved.
So instead make the next x value be LowerX + (UpperX”“LowerX) × Max[0.143, Min[0.857, LowerY/(LowerY”“UpperY) ]]
Repeat until UpperX”“LowerX ≤ Tolerance, that constant being pre-determined and small, at which time return the interpolated value (without the bounds).
When LowerX and UpperX are roughly even around the root, it interpolates. When one side is much closer, it brings in the other, moving it by a factor of 1÷0.143 ≈ 7.
FYI, the ‟0.143” constant came from a small experiment done in Excel. I do not know whether it should be precisely 1/7, or some other value. But a small non-exactitude in this would add only a tiny extra to the algorithm’s average time.
Indeed, this can be seen as a compromise between the slow robustness of interval bisection (‟! Max[0.5, Min[0.5, ! ]]”) and interpolation (‟! Max[0, Min[1, ! ]]”).
Assume root bounded by LowerX and UpperX, with matching y values LowerY and UpperY. Interpolation would make the next x value be LowerX + (UpperX”“LowerX) × LowerY/(LowerY”“UpperY). This can fail for some shapes (e.g., y = x^4 ”“ c), as the interpolated value is always on the same side of the root, so only one side (say, LowerX) ever gets moved.
So instead make the next x value be LowerX + (UpperX”“LowerX) × Max[0.143, Min[0.857, LowerY/(LowerY”“UpperY) ]]
Repeat until UpperX”“LowerX ≤ Tolerance, that constant being pre-determined and small, at which time return the interpolated value (without the bounds).
When LowerX and UpperX are roughly even around the root, it interpolates. When one side is much closer, it brings in the other, moving it by a factor of 1÷0.143 ≈ 7.
FYI, the ‟0.143” constant came from a small experiment done in Excel. I do not know whether it should be precisely 1/7, or some other value. But a small non-exactitude in this would add only a tiny extra to the algorithm’s average time.
Indeed, this can be seen as a compromise between the slow robustness of interval bisection (‟! Max[0.5, Min[0.5, ! ]]”) and interpolation (‟! Max[0, Min[1, ! ]]”).
Re: Software that makes placemats
Hmm... it does look a bit like a top down view of a Star Trek shuttlecraft... though /Galileo would probably be too esoteric of a reference.djewesbury wrote:I quickly discarded /BeetleCarapacePhilW wrote:Ditto. Some possible insect outlines came to mind, but ‟/DiamondsPlus” is probably simpler and clearer, and therefore preferred.Glenn E. wrote:I can think of nothing better.jdaw1 wrote:Current winner is ‟/DiamondsPlus”
Glenn Elliott
Re: Software that makes placemats
Not sure to which of the many possible uses of /Galileo this refers, but, as you say, too esoteric.Glenn E. wrote:Hmm... it does look a bit like a top down view of a Star Trek shuttlecraft... though /Galileo would probably be too esoteric of a reference.
- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Re: Software that makes placemats
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
jdaw1 wrote:Glenn E. wrote:too esoteric of a reference.
Re: Software that makes placemats
Different question. In the arrangement thread for the 1966 horizontal on 27th June, with each update of the placemats pictures have been posted in the thread.
E.g.,
E.g.,
Is this worth the effort?[url=http://www.theportforum.com/viewtopic.php?p=57931#p57931]Here[/url] jdaw1 wrote:Updated draft of the placemats.
- +BMHR and his Croft.

- djewesbury
- Graham’s 1970
- Posts: 8166
- Joined: 19:01 Mon 31 Dec 2012
- Location: Gothenburg, Sweden
- Contact:
Re: Software that makes placemats
yes
Daniel J.
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Husband of a relentless former Soviet Chess Master.
delete.. delete.. *sigh*.. delete...
Re: Software that makes placemats
jdaw1 wrote:with each update of the placemats pictures have been posted in the thread.
!
Is this worth the effort?
Agreed.djewesbury wrote:yes
"The first duty of Port is to be red"
Ernest H. Cockburn
Ernest H. Cockburn
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
In the general case I'd say no; It's useful in the case you refer to because the first post is not currently being regularly updated, so the image posts are providing a useful update of current attendees and ports; if the first post were being regularly updated, I think the additional effort of pdf -> jpg -> image hosting -> post for each placemat iteration would be excessive.jdaw1 wrote:Different question. In the arrangement thread for the 1966 horizontal on 27th June, with each update of the placemats pictures have been posted in the thread.
Is this worth the effort?
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
Presumably this also depends on any assumptions regarding the nature of the quartic to be solved, i.e. all-real roots (or at least a real root between the specified starting points), no discontinuities (no matching pole-zero root pairs) etc. In which case whether bisection, interpolation or your alternate specified scheme would be quicker in the general case would presumably depend on the nature of the group of potential curves across which the technique would be used? An alternative to the factor changed used to avoid never reaching the root could be to add a small proportion of the step delta determined from interpolation (deliberate over-adjust), though potentially decreasing the over-step with time to avoid oscillation; similar to techniques used to avoid getting stuck in local minima.jdaw1 wrote:Step one: write code to solve a quartic equation. Worrying, I think that I have devised an algorithm as good as Brent’s Method, but simpler, and not needing a pre-chosen x-step.
Assume root bounded by LowerX and UpperX, with matching y values LowerY and UpperY. Interpolation would make the next x value be LowerX + (UpperX”“LowerX) × LowerY/(LowerY”“UpperY). This can fail for some shapes (e.g., y = x^4 ”“ c), as the interpolated value is always on the same side of the root, so only one side (say, LowerX) ever gets moved.
So instead make the next x value be LowerX + (UpperX”“LowerX) × Max[0.143, Min[0.857, LowerY/(LowerY”“UpperY) ]]
Repeat until UpperX”“LowerX ≤ Tolerance, that constant being pre-determined and small, at which time return the interpolated value (without the bounds).
When LowerX and UpperX are roughly even around the root, it interpolates. When one side is much closer, it brings in the other, moving it by a factor of 1÷0.143 ≈ 7.
FYI, the ‟0.143” constant came from a small experiment done in Excel. I do not know whether it should be precisely 1/7, or some other value. But a small non-exactitude in this would add only a tiny extra to the algorithm’s average time.
Indeed, this can be seen as a compromise between the slow robustness of interval bisection (‟! Max[0.5, Min[0.5, ! ]]”) and interpolation (‟! Max[0, Min[1, ! ]]”).
Re: Software that makes placemats
Assumptions: ∈ ℝ; continuous; starting points either side. No more. Desiderata include robustness, speed, and simplicity of code.PhilW wrote:Presumably this also depends on any assumptions regarding the nature of the quartic to be solved, i.e. all-real roots (or at least a real root between the specified starting points), no discontinuities (no matching pole-zero root pairs) etc. In which case whether bisection, interpolation or your alternate specified scheme would be quicker in the general case would presumably depend on the nature of the group of potential curves across which the technique would be used? An alternative to the factor changed used to avoid never reaching the root could be to add a small proportion of the step delta determined from interpolation (deliberate over-adjust), though potentially decreasing the over-step with time to avoid oscillation; similar to techniques used to avoid getting stuck in local minima.
Don’t need to reach the root, only for the bounds either side to be closer than xTolerance, when do a final unconstrained linear interpolation.
-
PhilW
- Dalva Golden White Colheita 1952
- Posts: 3767
- Joined: 13:22 Wed 15 Dec 2010
- Location: Near Cambridge, UK
Re: Software that makes placemats
Any possibility of multiple roots between initial bounds (excluding duplicate root)? (I.e. can we either exclude the possibility of multiple roots being present, and If not then do we care? i.e. are all roots required, or any root). Could there be any bounding of the relative ratio of xTolerance to initial delta between upper and lower bounds?jdaw1 wrote:Assumptions: ∈ ℝ; continuous; starting points either side. No more. Desiderata include robustness, speed, and simplicity of code.
Don’t need to reach the root, only for the bounds either side to be closer than xTolerance, when do a final unconstrained linear interpolation.
n.b. I assume direct calculation would not be appropriate?