Page 23 of 27
Re: Software that makes placemats
Posted: 22:00 Sun 16 Jun 2019
by akzy
I used the placemats last night for a small tasting among a few physicists. Naturally, we decided to have field lines drawn on. I noted in the manual that Julian is displeased by these and whilst they are good for the majority of the page, some of the lines are non-physical (as circled).

- e field artifact.PNG (234.06 KiB) Viewed 80453 times
We then went on to discuss how we would do it ourselves (and is a similar method to how I create electric field simulations for trapped ions) . We believe the best option would be to treat each circle as a point charge and then create a potential map (i.e calculate the voltage across the sheet as superposition of each charge) for the entire sheet. From this grid, we can then perform some numerical differentiation (ideally if the point like nature is interpolated with a "reasonable order" function) to create a vector field (which would correspond to the electric field lines). As for visualization, the field lines would be the back-most image and the tasting circles would terminate drawing of lines such that the point charge wouldn't been seen.
Problems i foresee. How on earth do you,
1. Interpolate in PS
2. Differentiate in PS
3. Use PS
For my work I use Mathematica and its fantastic library of simple to use mathematical functions.
Re: Software that makes placemats
Posted: 22:53 Sun 16 Jun 2019
by jdaw1
• I dislike the whole
Rays algorithm. Despite the
previous discussion of it way back in summer 2013.
• You say that each circle should be a “point charge”. I suspect that aesthetically that wouldn’t work with the very strong circle motif. The lines need to leave the bounding circle, not a point charge within it. (But each circle cannot be a perfect conductor, as they touch, so would all be at the same charge.)
• Interpolate in Postscript … Differentiate in Postscript. Ans: do the work in Mathematica. Then output it in PostScript. Doh!
Code: Select all
(* PostScriptForm — this version of Jan 2019. *)
(* \
PostScriptForm[] *)
(*
\
http://mathematica.stackexchange.com/questions/101954/postscriptform-\
or-forthform
http://mathematica.stackexchange.com/questions/102894/multi-case-\
function-many-single-case-delayed-assignments-or-one-which
*)
Remove[PostScriptForm];
PostScriptForm[thing_Rational] :=
If[Abs[Denominator[
thing]/(2^IntegerExponent[Denominator[thing], 2])/(5^
IntegerExponent[Denominator[thing], 5])] == 1,
ToString[N[thing, 20], InputForm, NumberMarks -> False],
PostScriptForm[Numerator[thing]] <> " " <>
PostScriptForm[Denominator[thing]] <> " div"];
PostScriptForm[thing_?AtomQ] := ToString[thing];
PostScriptForm[thing_List] :=
StringJoin @@ Riffle[Map[PostScriptForm, thing], "\r\n"];
PostScriptForm[MatrixForm[thing_]] := PostScriptForm[thing];
PostScriptForm[Times[-1, thing_]] :=
StringJoin[PostScriptForm[thing], " neg"];
PostScriptForm[thing_Power] := (
psExponent := Which[
# > 5 && Divisible[#, 3],
psExponent[#/3] <> " dup dup mul mul",
# >= 5 && OddQ[#],
"dup " <> psExponent[(# - 1)/2] <> " dup mul mul" ,
# >= 4 && EvenQ[#], psExponent[#/2] <> " dup mul",
# == 3, "dup dup mul mul",
# == 2, "dup mul",
# == 1/2, "sqrt",
# == 3/2, "dup sqrt mul",
# < 0, psExponent[-#] <> " 1 exch div",
(Rational === Head[#]) && (Log[2, # // Denominator] //
IntegerQ), psExponent[Simplify[2 #]] <> " sqrt",
Not[IntegerQ[#]], PostScriptForm[#] <> " exp",
# == 1, "",
True,
" !!!\[Bullet]\[Bullet]\[Bullet]Error with exponent = " <>
ToString[#] <> "\[Bullet]\[Bullet]\[Bullet]!!! "
] &;
Which[
thing[[2]] > 0 || Not[IntegerQ[thing[[2]]]],
PostScriptForm[thing[[1]]] <> " " <> psExponent[thing[[2]]],
thing[[2]] == -1, "1 " <> PostScriptForm[thing[[1]]] <> " div",
thing[[2]] == 0, "1",
True,
"1 " <> PostScriptForm[thing[[1]]] <> " " <>
psExponent[-thing[[2]]] <> " div"
]);
PostScriptForm[thing_Times] :=
StringJoin@
Riffle[Reap[
If[MatchQ[thing[[1]],
Power[_,
n_Integer /; n < 0]], (Sow[
"1 " <> PostScriptForm[thing[[1, 1]]] <> " div"];), (Sow[
PostScriptForm[thing[[1]]]];)];
Map[(If[MatchQ[#,
Power[_,
n_Integer /; n < 0]], (Sow[
PostScriptForm[#[[1]]^(-#[[2]])] <> " div"];), (Sow[
PostScriptForm[#] <> " mul"]; )]) &,
Drop[List @@ thing, 1]]][[2, 1]], " "];
PostScriptForm[thing_Plus] :=
StringJoin @@ If[FreeQ[thing, _^n_],
(* Simple expression, no powers,
to be summed one item at a time *)
Module[{i},
i =
Position[thing, Except[Times[-1, _] | (_?Negative)], 1,
Heads -> False];
If[Length[i] > 0,
i = i[[1, 1]], (i =
Position[thing, Not[MatchQ[#, Times[-1, _]]] &, 1,
Heads -> False]; i = If[Length[i] > 0, i[[1, 1]], 1])];
Prepend[
Map[(" " <>
Replace[#, {(n_Integer /; n < 0 :>
ToString[-n] <> " sub"), (Times[-1, _] :>
PostScriptForm[Times @@ Drop[#, 1]] <> " sub"), (Times[
n_ /; n < 0, _] :>
PostScriptForm[Times @@ Drop[#, 1]] <> " " <>
ToString[-#[[1]]] <> " mul sub"), (Times[
n_ /; n > 0, _] :>
PostScriptForm[Times @@ Drop[#, 1]] <> " " <>
ToString[#[[1]]] <> " mul add"), (_ :>
PostScriptForm[#] <> " add")}]) &,
Drop[List @@ thing, {i}]],
Replace[thing[[
i]], {Times[-1, _] :>
PostScriptForm[-thing[[i]]] <> " neg", _ :>
PostScriptForm[thing[[i]]]}]] ],
(* Polynomial *)
Module[{vars, exps, v, rcl, i, firstMul},
vars = Variables[thing];
exps = Exponent[thing, vars];
v =
Select[Transpose[{vars, exps}], (#[[2]] == Max @@ exps) &][[1,
1]];
rcl = Reverse[Map[Factor, CoefficientList[thing, v]]];
Reap[
i = 1; firstMul = True;
If[rcl[[1]] =!= 1, Sow[PostScriptForm[rcl[[1]]]]];
Map[
If[# === 0,
i++, (Sow[
If[firstMul && rcl[[1]] === 1, PostScriptForm[v^i] <> " ",
" " <> PostScriptForm[v^i] <> " mul "] <>
If[MatchQ[#, (Times[_?Negative, _] | (_?Negative))],
PostScriptForm[-#] <> " sub",
PostScriptForm[#] <> " add"]]; i = 1;
firstMul = False)] &, Drop[rcl, 1]];
If[i > 1, Sow[" " <> PostScriptForm[v^(i - 1)] <> " mul "]];
][[2, 1]]
]];
(Did you really think that the
Temple calculations currently in lines 4918–4950 of
the code were written by hand?)
Re: Software that makes placemats
Posted: 23:32 Sun 16 Jun 2019
by akzy
So I had a quick play (please ignore the asymmetrical crimes against mathematics) around in mathematica doing a point charge simulation, see below for results. Depending on how the circle is placed over, I think it would look ok?
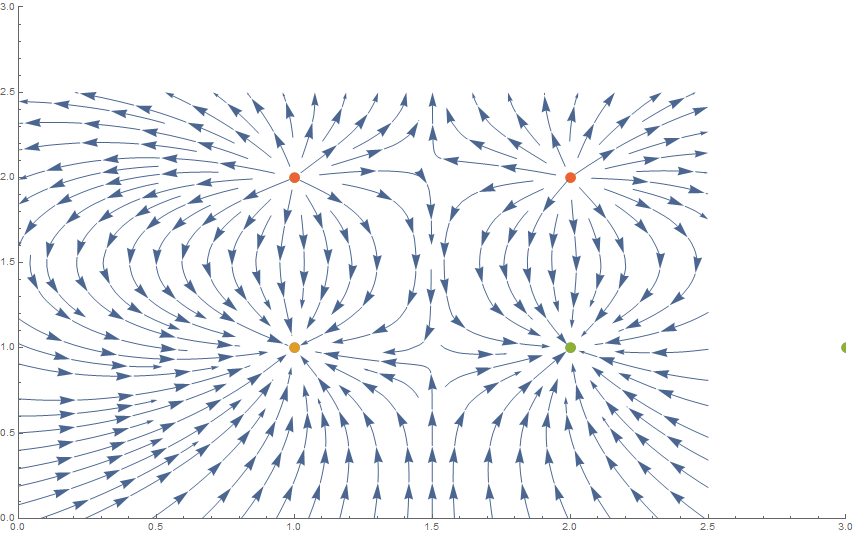
- pointcharge.png (118.88 KiB) Viewed 80436 times
I like the idea of doing it in Mathematica. I presume this is some sort of language converter?
Re: Software that makes placemats
Posted: 05:52 Mon 17 Jun 2019
by jdaw1
Interesting. What charge did you give each point? By what algorithm should the charges be chosen? And please post the code that made the diagram.
Re: Software that makes placemats
Posted: 18:02 Mon 17 Jun 2019
by akzy
Below is the code I used. I've changed things slightly so that it can all be solved analytically. Firstly, we define a series of vectors in circlepos which correspond to x,y and charge respectively. Set these however you please (I'd suggest arranging as a n/quadrupole- only because of the work i do
https://en.wikipedia.org/wiki/Quadrupole_ion_trap) . The function pot[] then calculates the potential (analytically). This is then summed over all potentials and differentiated in both x and y to produce the field in said directions. StreamPlot is then used to visualise it.
Code: Select all
circlepos = {{1, 1, 1}, {1, 2, -1}, {2, 1, 1}, {2, 2, -1}};
p1 = ListPlot[circlepos, PlotRange -> {{0, 3}, {0, 3}}];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2]
potgridx[x_, y_] =
D[Total[Table[
pot[x, y, circlepos[[i, 1]], circlepos[[i, 2]],
circlepos[[i, 3]]], {i, 1, Length[circlepos]}]], x];
potgridy[x_, y_] =
D[Total[Table[
pot[x, y, circlepos[[i, 1]], circlepos[[i, 2]],
circlepos[[i, 3]]], {i, 1, Length[circlepos]}]], y];
p2 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, 2.5}, {y, 0,
2.5}];
Show[p1, p2]
Re: Software that makes placemats
Posted: 20:04 Mon 17 Jun 2019
by jdaw1
akzy wrote: ↑23:32 Sun 16 Jun 2019I presume this is some sort of language converter?
Yes. Converts basic expressions to (slightly) idiomatic PostScript. Typical use case is a polynomial to be solved: it converts the
CoefficientList, which is then passed to a PostScript polynomial solver.
E.g.:
PostScriptForm[(a + Sqrt[b])^15] ➝
a b sqrt add dup dup mul dup mul mul dup dup mul mul
Your approach is well suited to circles in a rectangular grid. Not so much in a hexagonal grid. E.g.:
Code: Select all
circlepos = {
{0, 1, 1},
{Sqrt[3.]/2, 0.5, -1},
{Sqrt[3.]/2, -0.5, 1},
{0, -1, -1},
{-Sqrt[3.]/2, -0.5, 1},
{-Sqrt[3.]/2, 0.5, -1},
{0, 0, 1}
};
What might be need is some sort of chromatic / multi-dimensional field.
Re: Software that makes placemats
Posted: 21:10 Mon 17 Jun 2019
by akzy
jdaw1 wrote: ↑20:04 Mon 17 Jun 2019
E.g.:
PostScriptForm[(a + Sqrt[b])^15] ➝
a b sqrt add dup dup mul dup mul mul dup dup mul mul
Love it.
jdaw1 wrote: ↑20:04 Mon 17 Jun 2019
Your approach is well suited to circles in a rectangular grid. Not so much in a hexagonal grid. E.g.:
Code: Select all
circlepos = {
{0, 1, 1},
{Sqrt[3.]/2, 0.5, -1},
{Sqrt[3.]/2, -0.5, 1},
{0, -1, -1},
{-Sqrt[3.]/2, -0.5, 1},
{-Sqrt[3.]/2, 0.5, -1},
{0, 0, 1}
};
Fixed.
Code: Select all
circlevec = {{0, 1, 1}, {Sqrt[3.]/2, 0.5, -1}, {Sqrt[3.]/2, -0.5,
1}, {0, -1, -1}, {-Sqrt[3.]/2, -0.5, 1}, {-Sqrt[3.]/2,
0.5, -1}, {0, 0, 1}};
circlepos =
Table[{circlevec[[i, 1]], circlevec[[i, 2]]}, {i, 1,
Length[circlevec]}];
p1 = ListPlot[circlepos, PlotRange -> {{-2.5, 2.5}, {-2.5, 2.5}},
PlotMarkers -> {Automatic, Large}];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2]
potgridx[x_, y_] =
D[Total[Table[
pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]],
circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], x];
potgridy[x_, y_] =
D[Total[Table[
pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]],
circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], y];
p2 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, -2.5,
2.5}, {y, -2.5, 2.5}];
Show[p1, p2]
And for those who aren't blessed with Mathematica,
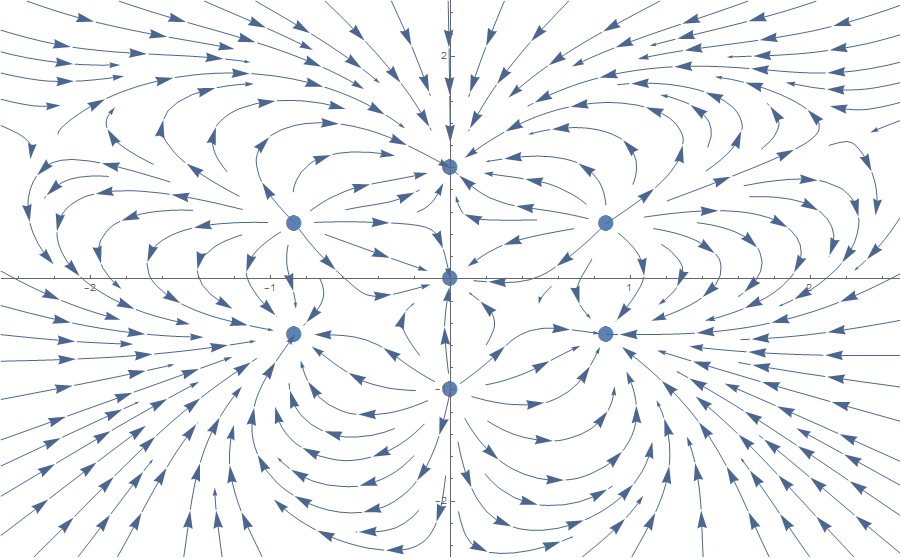
- hexcharge.png (148.06 KiB) Viewed 80307 times
Re: Software that makes placemats
Posted: 21:45 Mon 17 Jun 2019
by jdaw1
akzy wrote: ↑21:10 Mon 17 Jun 2019jdaw1 wrote: ↑20:04 Mon 17 Jun 2019E.g.:
PostScriptForm[(a + Sqrt[b])^15] ➝
a b sqrt add dup dup mul dup mul mul dup dup mul mul
Love it.
So do I, but perhaps more for its wilful stubbornness than its practicality.
akzy wrote: ↑21:10 Mon 17 Jun 2019Fixed.
Hmm. Bug or feature?
• The points south, east-by-north-east and west-by-north-west relate well to the central circle.
• But the points north, east-by-south-east and west-by-south-west do not connect to the central circle at all.
For my palate, this is an offence to symmetry. There’s no
a priori reason for the central circle to exhibit such favouritism. You’re trying to squeeze a 2ⁿ pattern into a shape divisible by three, and I think it doesn’t fit.
Others: please take sides.
Some circle arrangements to consider (ignore the decorations):
I repeat:
jdaw1 wrote: ↑05:52 Mon 17 Jun 2019By what algorithm should the charges be chosen?
Display: inside the circles is different to outside. Perhaps it should be shown inside faded 60%; and outside at full strength? Comment and recommendation welcomed.
Re: Software that makes placemats
Posted: 22:28 Mon 17 Jun 2019
by akzy
Obviously a feature.
With the asymmetry, it is bothering me too. I have a suspicion that it's because we're working up against imperfect machine precision. If you plot symmetries in along one plane, you might notice there's a field preference to one side. Perhaps the numbers will have to be adjusted so that they can be positions with exact machine precision? I'll have a play and see what I can muster up.
I'll have a look at some previous placemats soon, see what can be made.
As for the algorithm, I'm really not sure. At least there is a flexibility to have any charge (or even strength of charge for that extra special something).
Re: Software that makes placemats
Posted: 22:35 Mon 17 Jun 2019
by jdaw1
FYI, the only floating-point precision in PostScript is
single: 23-bit mantissa ≈ one part in eight million; 8 bits exponent so maximum value ≈ ±10³⁸.
Re: Software that makes placemats
Posted: 22:39 Mon 17 Jun 2019
by akzy
jdaw1 wrote: ↑22:35 Mon 17 Jun 2019
FYI, the only floating-point precision in PostScript is
single: 23-bit mantissa ≈ one part in eight million; 8 bits exponent so maximum value ≈ ±10³⁸.
Ok, I will try zeroing at 2^-23.
I also had a little play with some other fun field related plots (whilst trying to diagnose). Whilst just a first attempt, and numbers will have to be fudged to make it look better,
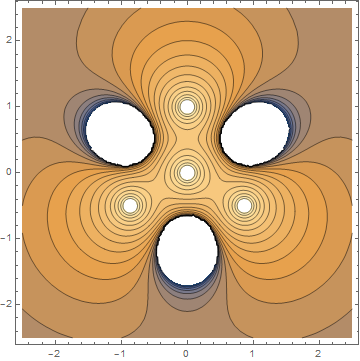
- contourpot.png (72.51 KiB) Viewed 80246 times
Plotted using
Code: Select all
ContourPlot[
Log[Total[
Table[pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]],
circlevec[[i, 3]]], {i, 1, Length[circlevec]}]]], {x, -2.5,
2.5}, {y, -2.5, 2.5}, Contours -> 20]
Re: Software that makes placemats
Posted: 07:20 Tue 18 Jun 2019
by PhilW
jdaw1 wrote: ↑21:45 Mon 17 Jun 2019Hmm. Bug or feature?
• The points south, east-by-north-east and west-by-north-west relate well to the central circle.
• But the points north, east-by-south-east and west-by-south-west do not connect to the central circle at all.
From the imagery, would I be correct in thinking that each point represents a certain positive or negative charge, and therefore that the reason some points connect to others while others pairs to not is that essentially we are only seeing lines between points of opposite (or different) charge? If so, some variation from binary charge setting would enable alternate maps with all points connecting, though would be potentially difficult to keep regular and symmetrical for all designs without specific rules.
Based on the above, but varying slightly, would making the centre of all circles could be a positive charge, and then placing negative charges between (either in the spaces or the mid-point between adjacent circles) might provide a more fully-connected and symmetric output, though I can't picture whether that might become too linear.
Re: Software that makes placemats
Posted: 11:01 Tue 18 Jun 2019
by akzy
PhilW wrote: ↑07:20 Tue 18 Jun 2019
From the imagery, would I be correct in thinking that each point represents a certain positive or negative charge, and therefore that the reason some points connect to others while others pairs to not is that essentially we are only seeing lines between points of opposite (or different) charge? If so, some variation from binary charge setting would enable alternate maps with all points connecting, though would be potentially difficult to keep regular and symmetrical for all designs without specific rules.
Based on the above, but varying slightly, would making the centre of all circles could be a positive charge, and then placing negative charges between (either in the spaces or the mid-point between adjacent circles) might provide a more fully-connected and symmetric output, though I can't picture whether that might become too linear.
Good idea. I also changed circlepos to a different hexagonal lattice..
Code: Select all
{{0, 2 Sqrt[2], -1}, {Sqrt[2], Sqrt[2], -1}, {-Sqrt[2],
Sqrt[2], -1}, {0, -2 Sqrt[2], -1}, {-Sqrt[2], -Sqrt[2], -1}, {Sqrt[
2], -Sqrt[2], -1}, {0, 0, 1}}
Re: Software that makes placemats
Posted: 19:39 Tue 18 Jun 2019
by jdaw1
akzy wrote: ↑11:01 Tue 18 Jun 2019Good idea. I also changed circlepos to a different hexagonal lattice.
Charges good. Because circles touch, hexagonal was better.
How to generalise the charges it to fit
jdaw1 wrote: ↑21:45 Mon 17 Jun 2019
For this type of layout, might a triangle tesselation with charges {⅓,⅔,1} be correct?
Code: Select all
circlevec = {
{0, 1, 1},
{Sqrt[3.]/2, 0.5, 1/3},
{Sqrt[3.]/2, -0.5, 1},
{0, -1, 1/3},
{-Sqrt[3.]/2, -0.5, 1},
{-Sqrt[3.]/2, 0.5, 1/3},
{0, 0, 2/3}
};
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, 0.5]}] &, circlevec[[All, 1 ;; 2]]];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] =
D[Total[Table[
pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]],
circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], x];
potgridy[x_, y_] =
D[Total[Table[
pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]],
circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], y];
p2 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, -1.6,
1.6}, {y, -1.6, 1.6}];
Show[p1, p2, AspectRatio -> 1]
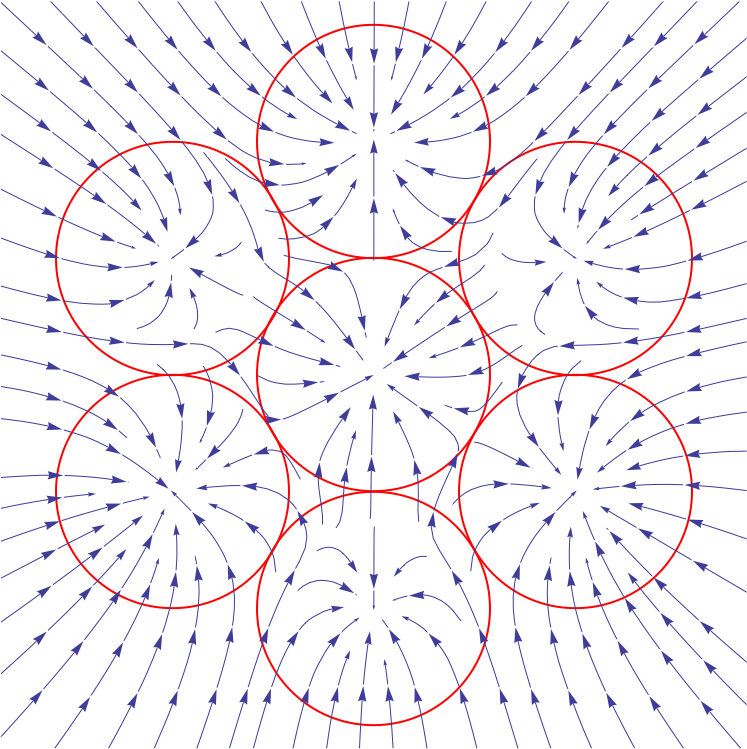
(Alas my Mathematica v9 can’t specify
StreamMarkers -> "Segment".)
Re: Software that makes placemats
Posted: 22:17 Tue 18 Jun 2019
by jdaw1
Edited Wed 19th June to rename Dists ➝ Pot. Please, no jokes.
Possible algorithm for assigning charges
Circles either have a charge assigned (hurray!), which is one of {1,2,3}. Or don’t yet, in which case deemed charge is 0.
Repeatedly we’ll compute, for circle i, Poti0, Poti1, Poti2, and Poti3.
Potik ≡ ∑j ( (xi − xj)² + (yi − yj)² )⁻¹ where j≠i and circle j has charge k.
Pick of the i with no assigned charge the largest value of Poti0÷1024 + Poti1 + Poti2 + Poti3
Assign to it the the charge {3,1,2} according to whichever is smallest of Poti3, Poti1, Poti2, with ties being resolved in that order.
Repeat until all charges assigned.
Observe: easy to code; O(n³) which is acceptable with n≤24; effectively maximises distance between similar charges; starts in centre and chooses circles adjacent to those with known charge, working outwards.
Good? Bad? Improvements?
(But I still have no idea how to compute the streams. Help!)
Re: Software that makes placemats
Posted: 17:05 Wed 19 Jun 2019
by akzy
jdaw1 wrote: ↑19:39 Tue 18 Jun 2019
Charges good. Because circles touch, hexagonal was better.
I never said it was an efficient packing

- either way, looks like its producing decent results. As for the charges it may start to look a bit funky on large arrays due to edge effects and failing large scale symmetry. I think the solution is "have a play around".
As for you algorithm, it seems good. I think seeing it in action will let us know how well it looks.
For manually making a StreamPlot (I think this is what you meant?) I imagine that will be tougher. What I suggest is that we...
1. Create field seed spots at the edges of the circles (at whatever density we decide).
2. At that point, we have a vector (from potgridx and potgridy) telling us where the field goes next.
3. Follow that on some small distance (there is definitely a mathematical way of determining how small this distance is - I cant' remember however).
4. Return back to step 2 until you're off the mat or in another circle.
5. Fit a curve to each trace.
I'm a touch busy atm with pesky thesis writing (
we'll forget about a week in Provence coming soon) but if I get some time, I can try have a play with it.
Re: Software that makes placemats
Posted: 19:53 Wed 19 Jun 2019
by jdaw1
akzy wrote: ↑17:05 Wed 19 Jun 2019For manually making a StreamPlot (I think this is what you meant?) I imagine that will be tougher.
I am absolutely sure it will be very tricky.
akzy wrote: ↑17:05 Wed 19 Jun 2019Create field seed spots at the edges of the circles (at whatever density we decide).
Or choose seed points in a small circle around a charge, perhaps every 15°. Flow uphill. But those won’t arrive at even angles at other charges, nor at even distances at edge. Then what? I don’t know.
Also, can the flow uphill be ‘locally’ analytic? If it could be known quite well over a moderate distance, that could be converted to a single Bézier cubic using
ApproximatingCurve.
Re: Software that makes placemats
Posted: 15:07 Thu 20 Jun 2019
by Alex Bridgeman
jdaw1 wrote: ↑21:45 Mon 17 Jun 2019
Others: please take sides.
Sorry? Did someone say something?
Wake me up when it's over and someone can explain in English what just happened...
Re: Software that makes placemats
Posted: 22:29 Thu 20 Jun 2019
by jdaw1
jdaw1 wrote: ↑22:17 Tue 18 Jun 2019Possible algorithm for assigning charges
Circles either have a charge assigned (hurray!), which is one of {1,2,3}. Or don’t yet, in which case deemed charge is 0.
Repeatedly we’ll compute, for circle
i, Pot
i0, Pot
i1, Pot
i2, and Pot
i3.
Pot
ik ≡ ∑
j ( (
xi −
xj)² + (
yi −
yj)² )⁻¹ where
j≠
i and circle
j has charge
k.
Pick of the
i with no assigned charge the largest value of Pot
i0÷1024 + Pot
i1 + Pot
i2 + Pot
i3
Assign to it the the charge {3,1,2} according to whichever is smallest of Pot
i3, Pot
i1, Pot
i2, with ties being resolved in that order.
Repeat until all charges assigned.
Test implementation of the charge assignment:
output looks good — nearby circles have different charges; PostScript code follows.
Code: Select all
/ParametersVersionDateTimeAdobeFormat (D:201906202330) def
/Circlearrays [ [/lozenge] 15 {dup} repeat pop ] def
/Titles [ ( ) 15 {dup} repeat pop ] def
/Belowtitles [ Titles length {()} repeat ] def
/Names [
(JDAW)
] def
/HeadersLeft [
0 [(Assigning charges: a test)]
] def % /HeadersLeft
/HeadersCenter [
] def % /HeadersCenter
/HeadersRight [
0
{ExternalLinks 2 get}
] def % /HeadersRight
/ExternalLinks [ % Array, length a multiple of three: indented0-boolean, (Descriptor0), (http://URL0), indented1-boolean, (Descriptor1), (http://URL1), ...
false (Thread on ThePortForum.com) (http://www.theportforum.com/viewtopic.php?t=175&start=1136#p112232)
false (Algorithm on ThePortForum.com) (http://www.theportforum.com/viewtopic.php?p=112250#p112250)
false (Latest version this placemat) (http://www.jdawiseman.com/papers/2019/20190620_Charges.pdf)
] def % /ExternalLinks
/VoteRecorders false def
/CorkDisplayNumCopies 0 def
/NeckTagsNumCopies 0 def
/DecantingNotesNumCopies 0 def
/TastingNotePagesNumCopies 0 def
/PaperType { [ /A3 /A4 dup dup dup /A3 dup dup dup] SheetNum get } def
/Orientation {SheetNum 1 eq SheetNum 2 eq or {/Portrait} {/Landscape} ifelse} def % /Landscape /Portrait
/GlassesOnSheets [
[ 7 5 6 5 7 11 13 14 15 ]
{ [ exch 0 exch 1 exch 1 sub {} for ] }
forall
] def % /GlassesOnSheets
/ShrinkRadii /NotAtAll def % /NotAtAll | /ToSmallest | /ToSmallestSamePageOrdering | array denoting equivalence classes
/PackingStyles [
[ /RectangularDislocation /OnlyIfSheetNumMin 1 ]
[ /Diamonds /OnlyIfSheetNumMin 1 ]
[ /DiamondsAndRectangular /OnlyIfSheetNumMin 1 ]
[ /Bespoke5 /OnlyIfOrientation /Landscape /OnlyIfSheetNumMin 1 ]
[ /Bespoke7 /OnlyIfOrientation /Landscape/OnlyIfSheetNumMin 1 ]
[ /RectangularAlternateSplitNudge /OnlyIfSheetNumMin 1 /ImprovementPointsMin 2 ]
[ /DiamondsPlus /OnlyIfOrientation /Portrait /OnlyIfSheetNumMin 1 ]
[ /DiamondsPlus /OnlyIfOrientation /Landscape /OnlyIfSheetNumMin 1 /ImprovementPointsMin 2 ]
[ /RectangularAlternateNudge /OnlyIfSheetNumMin 1 /ImprovementPointsMin 2 ]
[ /Arch /CentralGlasses 1 /GlassesNumMin 6 /OnlyIfOrientation /Landscape ]
] def % /PackingStyles
/PaintBackgroundCode
{
% Done properly, the computations would be in PrologueCode, and only the painting in PaintBackgroundCode.
/Glasses TypeOfPagesBeingRendered eq
{
10 dict begin
/N1s GlassPositions SheetNum get length 1 sub def
/Xs [ GlassPositions SheetNum get {0 get} forall ] def
/Ys [ GlassPositions SheetNum get {1 get} forall ] def
/Charges [ 0 N1s {dup} repeat ] def
/Title 1 string def Title 0 65 put
N1s 1 add
{
/Pot [ 4 { [ 0 N1s {dup} repeat ] } repeat ] def
0 1 N1s
{
/i exch def
0 1 N1s
{
/j exch def
i j ne
{
Pot Charges j get get i 2 copy get 1 Xs i get Xs j get sub dup mul Ys i get Ys j get sub dup mul add div add put
} if % i j ne
} for % j
} for % i
/PotMax -1 def
/iBest -1 def
0 1 N1s
{
/i exch def
Charges i get 0 eq
{
Pot 0 get i get 1024 div Pot 1 get i get add Pot 2 get i get add Pot 3 get i get add
dup PotMax gt {/PotMax exch def /iBest i def} {pop} ifelse
} if % Charges i get 0 eq
} for % i
Charges iBest
Pot 3 get iBest get Pot 1 get iBest get le
{Pot 3 get iBest get Pot 2 get iBest get le {3} {2} ifelse}
{Pot 1 get iBest get Pot 2 get iBest get le {1} {2} ifelse}
ifelse put
TitlesFont RadiiCirclearrayInside SheetNum get 1.9 mul selectfont
GlassPositions SheetNum get iBest get aload pop moveto
GSave nulldevice 0 0 moveto Title false CharPathRecursive PathBBox GRestore exch 4 -1 roll add -2 div 3 1 roll add -2 div rmoveto
[ {/Error} {0.8 setgray} {0.4 0.4 0.5 setrgbcolor} {0.6 0 0 setrgbcolor} ] Charges iBest get get exec
Title ShowRecursive
Title 0 2 copy get 1 add put
} repeat
end
} if
} bind def
But the charge assignment is the easy bit. Making the streams will be much much more tricky.
Re: Software that makes placemats
Posted: 16:01 Sun 23 Jun 2019
by jdaw1
More realistic example at
jdawiseman.com/2019/20190623_Rays_A4.nb.
Code: Select all
h = 297 (360/127) - 30 - 24;
w = 210 (360/127) - 24 - 24;
r = w/4;
Clear["yy"]; yy = yy /. Solve[(yy - r)^2 == (h - r - yy)^2 + (w/2 - r)^2, yy][[1]];
Print["h=", h, " w=", w, " r=", r, " yy=", yy];
Print[N[circlevec = {
{w/2, h - r, 2},
{r, yy, 3},
{w - r, yy, 1},
{r, r, 2},
{w - r, r, 3}
}] // MatrixForm];
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, r]}] &, circlevec[[All, 1 ;; 2]]];
p2 = Graphics[Map[Text[Style[#[[3]], FontSize -> 60, Bold, Green], {#[[1]], #[[2]]}, {0, 0}] &, circlevec]];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] = D[Total[Table[pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]], circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], x];
potgridy[x_, y_] = D[Total[Table[pot[x, y, circlevec[[i, 1]], circlevec[[i, 2]], circlevec[[i, 3]]], {i, 1, Length[circlevec]}]], y];
p3 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, w}, {y, 0, h}];
Show[p1, p2, p3, AspectRatio -> h/w]
In the picture green numbers are the charges.
If only
StreamPlot weren’t so fiercely difficult to re-code.
Re: Software that makes placemats
Posted: 20:23 Sun 23 Jun 2019
by PhilW
A suggestion for alternate charge-plan to try and regularise:
- For every circle, inscribe a hexagon (possibly slightly smaller diameter).
- Assign charge to hexagon points (instead of circle centres), all with +1 at top point, then alternating -1/+1 around the hexagon.
In any square or hexagonal arrangement of circles, that should avoid like charges bring close, allowing good connectivity between, while also being regular/simple charge definition for all layouts.
Re: Software that makes placemats
Posted: 20:24 Sun 23 Jun 2019
by PhilW
If only StreamPlot weren’t so fiercely difficult to re-code.
Do you have a pseudo-code algorithm?
Re: Software that makes placemats
Posted: 19:57 Mon 24 Jun 2019
by jdaw1
PhilW wrote: ↑20:23 Sun 23 Jun 2019A suggestion for alternate charge-plan to try and regularise:
- For every circle, inscribe a hexagon (possibly slightly smaller diameter).
- Assign charge to hexagon points (instead of circle centres), all with +1 at top point, then alternating -1/+1 around the hexagon.
In any square or hexagonal arrangement of circles, that should avoid like charges bring close, allowing good connectivity between, while also being regular/simple charge definition for all layouts.
Interesting. I will test. Might the mesh of points be too fine — points too close — such that it loses the macro structure?
PhilW wrote: ↑20:24 Sun 23 Jun 2019If only StreamPlot weren’t so fiercely difficult to re-code.
Do you have a pseudo-code algorithm?
No.
Re: RE: Re: Software that makes placemats
Posted: 20:03 Mon 24 Jun 2019
by PhilW
jdaw1 wrote:Interesting. I will test. Might the mesh of points be too fine — points too close — such that it loses the macro structure?
My gut feel was that it should be viable for hexagons, but that moving to decagons or higher 2*oddN sided polygons would be too fine. Might/not work, but thought worth suggesting to try.
Re: Software that makes placemats
Posted: 22:26 Mon 24 Jun 2019
by jdaw1
.nbCode: Select all
h = 297 (360/127) - 30 - 24;
w = 210 (360/127) - 24 - 24;
r = w/4;
Clear["yy"]; yy =
yy /. Solve[(yy - r)^2 == (h - r - yy)^2 + (w/2 - r)^2, yy][[1]];
Print["h=", h, " w=", w, " r=", r, " yy=", yy];
Print[N[circleCentres = {
{w/2, h - r},
{r, yy},
{w - r, yy},
{r, r},
{w - r, r}
}] // MatrixForm];
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, r]}] &,
circleCentres];
charges = Flatten[Map[{
{#[[1]], #[[2]] + r, +1},
{#[[1]] + r Sqrt[3]/2, #[[2]] + r/2, -1},
{#[[1]] + r Sqrt[3]/2, #[[2]] - r/2, +1},
{#[[1]], #[[2]] - r, -1},
{#[[1]] - r Sqrt[3]/2, #[[2]] - r/2, +1},
{#[[1]] - r Sqrt[3]/2, #[[2]] + r/2, -1}
} &, circleCentres], 1];
p2 = Map[Graphics[{Green, Thick, Circle[{#[[1]], #[[2]]}, r/48]}] &,
charges];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] =
D[Total[Table[
pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i,
1, Length[charges]}]], x];
potgridy[x_, y_] =
D[Total[Table[
pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i,
1, Length[charges]}]], y];
p3 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, w}, {y, 0,
h}];
Show[p1, p2, p3, AspectRatio -> h/w]
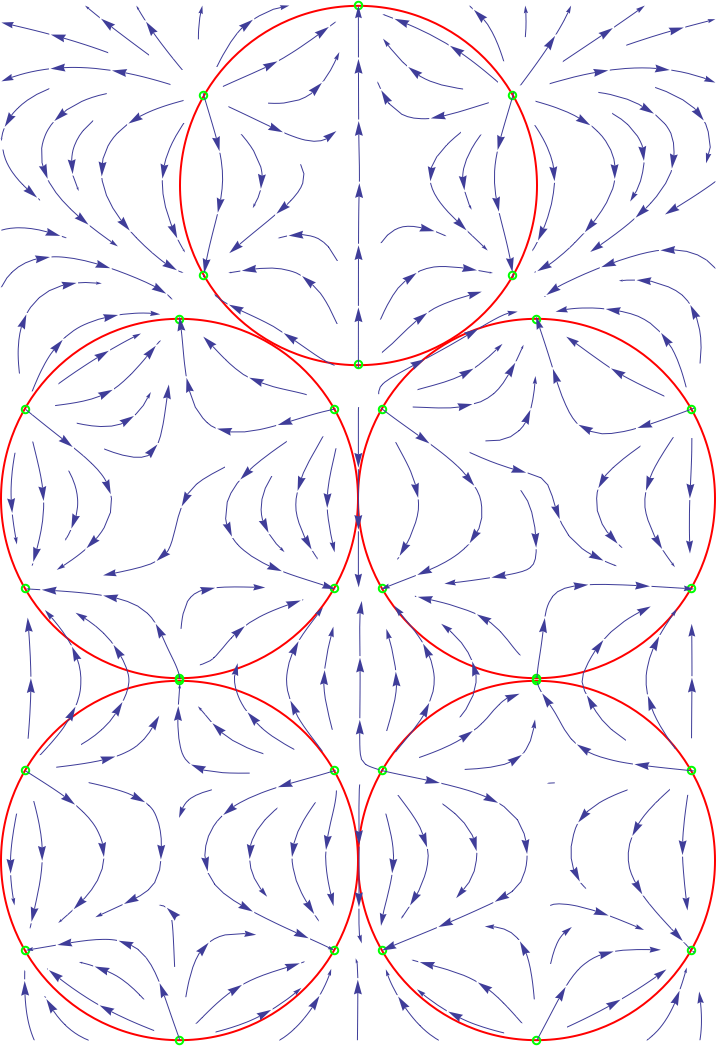
Re: Software that makes placemats
Posted: 22:27 Mon 24 Jun 2019
by jdaw1
.nbCode: Select all
h = 297 (360/127) - 30 - 24;
w = 210 (360/127) - 24 - 24;
r = w/4;
Clear["yy"]; yy =
yy /. Solve[(yy - r)^2 == (h - r - yy)^2 + (w/2 - r)^2, yy][[1]];
Print["h=", h, " w=", w, " r=", r, " yy=", yy];
Print[N[circleCentres = {
{w/2, h - r},
{r, yy},
{w - r, yy},
{r, r},
{w - r, r}
}] // MatrixForm];
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, r]}] &,
circleCentres];
charges = Flatten[Map[{
{#[[1]], #[[2]] + r, +1},
{#[[1]] + r, #[[2]], -1},
{#[[1]], #[[2]] - r, +1},
{#[[1]] - r, #[[2]], -1}
} &, circleCentres], 1];
p2 = Map[Graphics[{Green, Thick, Circle[{#[[1]], #[[2]]}, r/48]}] &,
charges];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] =
D[Total[Table[
pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i,
1, Length[charges]}]], x];
potgridy[x_, y_] =
D[Total[Table[
pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i,
1, Length[charges]}]], y];
p3 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, w}, {y, 0,
h}];
Show[p1, p2, p3, AspectRatio -> h/w]
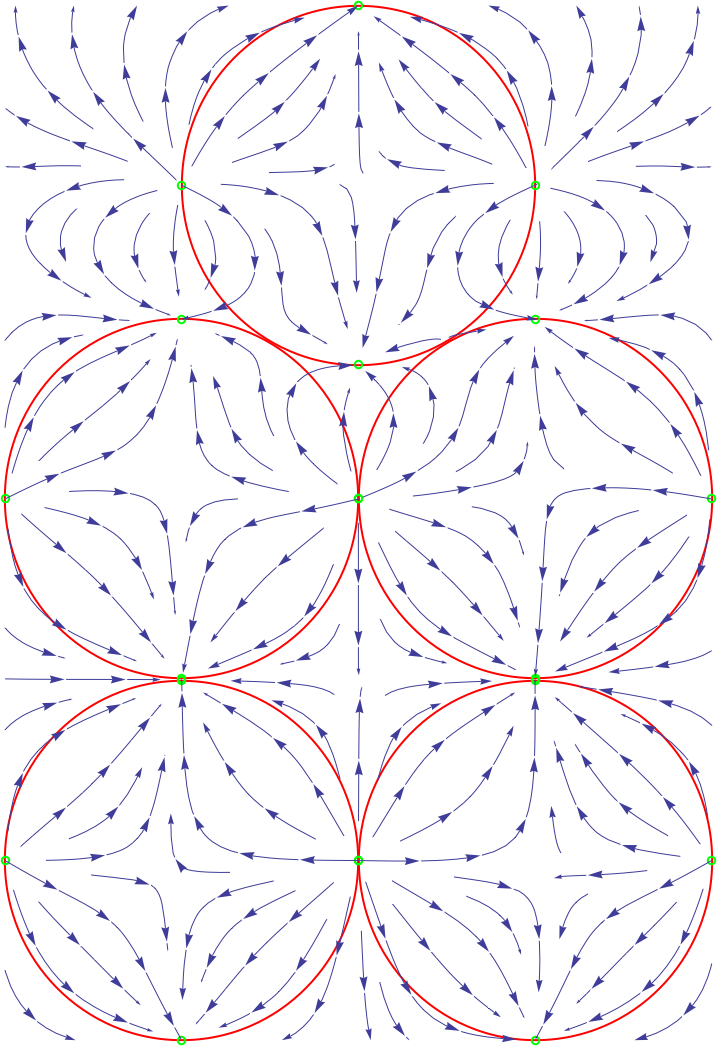
Re: Software that makes placemats
Posted: 22:30 Mon 24 Jun 2019
by jdaw1
All this is conditional in being able to implement StreamPlot. Subject to which, do we want the average charge to be zero, or to have the inward flow from all charges being positive?
Also, is Phil’s plan too symmetrical. Does the rigorous symmetry cause non-interestingness?
Re: Software that makes placemats
Posted: 16:34 Wed 26 Jun 2019
by akzy
Are you able to implement python in postscript? If so matplotlib has the stream plot coded out for you
https://github.com/matplotlib/matplotli ... eamplot.py
Another option is manually translate into whatever language.
Re: Software that makes placemats
Posted: 22:17 Thu 27 Jun 2019
by jdaw1
{Shudder} Translating that to PostScript would likely as not be 3k lines. {Shudder}
Re: Software that makes placemats
Posted: 06:55 Fri 28 Jun 2019
by PhilW
The first of your two examples does set the charges on hexagonal points as suggested, but puts them on the circle perimeter - I think it would work better if they were at ~85% of the radius.
Re: Software that makes placemats
Posted: 22:56 Fri 28 Jun 2019
by jdaw1
PhilW wrote: ↑06:55 Fri 28 Jun 2019The first of your two examples does set the charges on hexagonal points as suggested, but puts them on the circle perimeter - I think it would work better if they were at ~85% of the radius.
.nbCode: Select all
h = 297 (360/127) - 30 - 24;
w = 210 (360/127) - 24 - 24;
r = w/4;
rr = 0.85 r;
Clear["yy"]; yy =
yy /. Solve[(yy - r)^2 == (h - r - yy)^2 + (w/2 - r)^2, yy][[1]];
Print["h=", h, " w=", w, " r=", r, " yy=", yy];
Print[N[circleCentres = {
{w/2, h - r},
{r, yy},
{w - r, yy},
{r, r},
{w - r, r}
}] // MatrixForm];
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, r]}] &,
circleCentres];
charges = Flatten[Map[{
{#[[1]] , #[[2]] + rr, +1},
{#[[1]] + rr Sqrt[3]/2, #[[2]] + rr/2, -1},
{#[[1]] + rr Sqrt[3]/2, #[[2]] - rr/2, +1},
{#[[1]] , #[[2]] - rr, -1},
{#[[1]] - rr Sqrt[3]/2, #[[2]] - rr/2, +1},
{#[[1]] - rr Sqrt[3]/2, #[[2]] + rr/2, -1}
} &, circleCentres], 1];
p2 = Map[Graphics[{Green, Thick, Circle[{#[[1]], #[[2]]}, r/48]}] &, charges];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] = D[Total[Table[pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i,1, Length[charges]}]], x];
potgridy[x_, y_] = D[Total[Table[pot[x, y, charges[[i, 1]], charges[[i, 2]],charges[[i, 3]]], {i, 1, Length[charges]}]], y];
p3 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, w}, {y, 0, h}];
Show[p1, p2, p3, AspectRatio -> h/w]
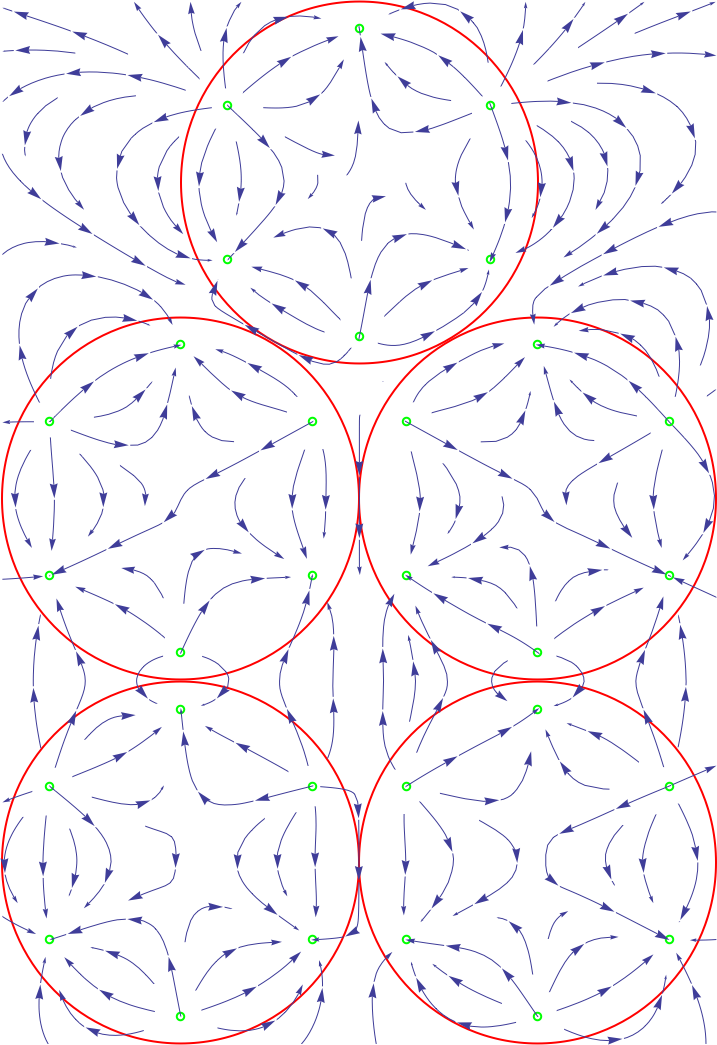
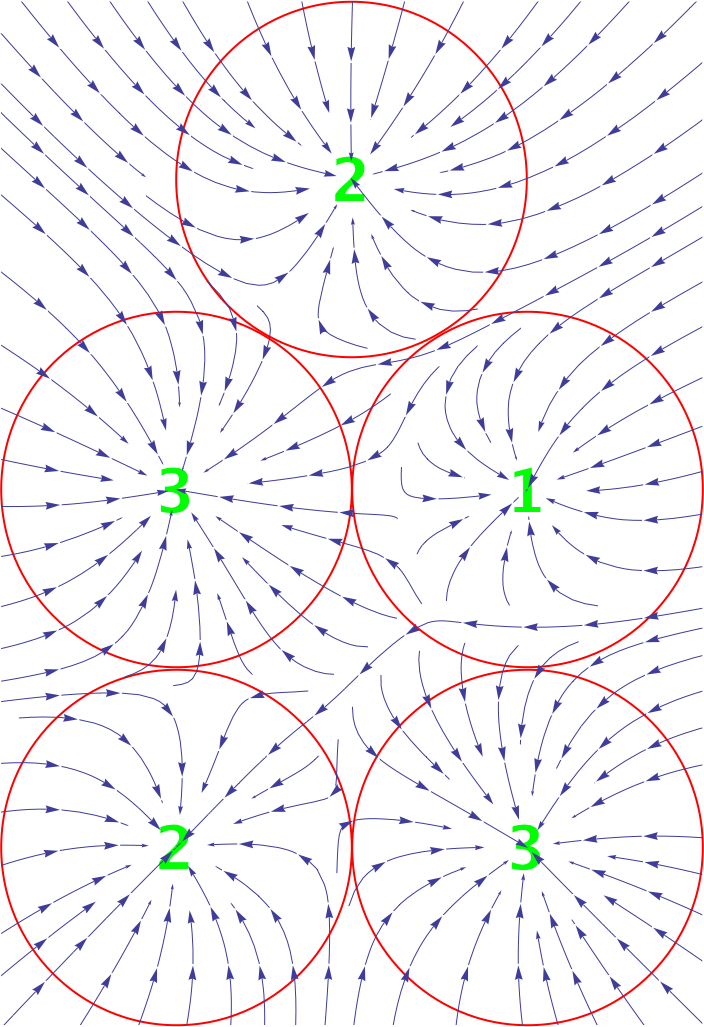
I prefer:
jdaw1 wrote: ↑16:01 Sun 23 Jun 2019
Why? The inward pointing of the lines, the sitting in its own gravitational well, has the outside pointing to the important stuff — the juice. Within which I like the visual interest of not having macro symmetry. And the fewness of the lines hides the micro structure of 6× as many charges.
Re: Software that makes placemats
Posted: 05:46 Sat 29 Jun 2019
by PhilW
jdaw1 wrote: ↑22:56 Fri 28 Jun 2019I prefer:
jdaw1 wrote: ↑16:01 Sun 23 Jun 2019
Why? The inward pointing of the lines, the sitting in its own gravitational well, has the outside pointing to the important stuff — the juice. Within which I like the visual interest of not having macro symmetry. And the fewness of the lines hides the micro structure of 6× as many charges.
I agree with the preference, because of the inward/outward pointing of the lines, though I would also prefer macro symmetry; I was hoping to achieve the former with the regular hexagon plan by moving the charges further inside, but alas that doesn't seem sufficient.
Re: Software that makes placemats
Posted: 09:04 Sat 29 Jun 2019
by jdaw1
PhilW wrote: ↑05:46 Sat 29 Jun 2019I agree with the preference, because of the inward/outward pointing of the lines, though I would also prefer macro symmetry; I was hoping to achieve the former with the regular hexagon plan by moving the charges further inside, but alas that doesn't seem sufficient.
First (
.nb) has shuffled charges, integers from half the number of glasses to 1½× that.
Code: Select all
h = 297 (360/127) - 30 - 24;
w = 210 (360/127) - 24 - 24;
r = w/4;
Clear["yy"]; yy = yy /. Solve[(yy - r)^2 == (h - r - yy)^2 + (w/2 - r)^2, yy][[1]];
Print["h=", h, " w=", w, " r=", r, " yy=", yy];
Print[N[circleCentres = {
{w/2, h - r},
{r, yy},
{w - r, yy},
{r, r},
{w - r, r}
}] // MatrixForm];
charges = Transpose[Join[Transpose[circleCentres], {RandomSample[Floor[Length[circleCentres]/2] + Range[Length[circleCentres]]]}]];
p1 = Map[Graphics[{Red, Thick, Circle[{#[[1]], #[[2]]}, r]}] &, circleCentres];
p2 = Graphics[ Map[Text[Style[#[[3]], FontSize -> 60, Bold, Green], {#[[1]], #[[2]]}, {0, 0}] &, charges]];
pot[x_, y_, qx_, qy_, q_] := q/Sqrt[(x - qx)^2 + (y - qy)^2];
potgridx[x_, y_] = D[Total[Table[pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i, 1, Length[charges]}]], x];
potgridy[x_, y_] = D[Total[Table[pot[x, y, charges[[i, 1]], charges[[i, 2]], charges[[i, 3]]], {i, 1, Length[charges]}]], y];
p3 = StreamPlot[{potgridx[x, y], potgridy[x, y]}, {x, 0, w}, {y, 0, h}];
Show[p1, p2, p3, AspectRatio -> h/w]
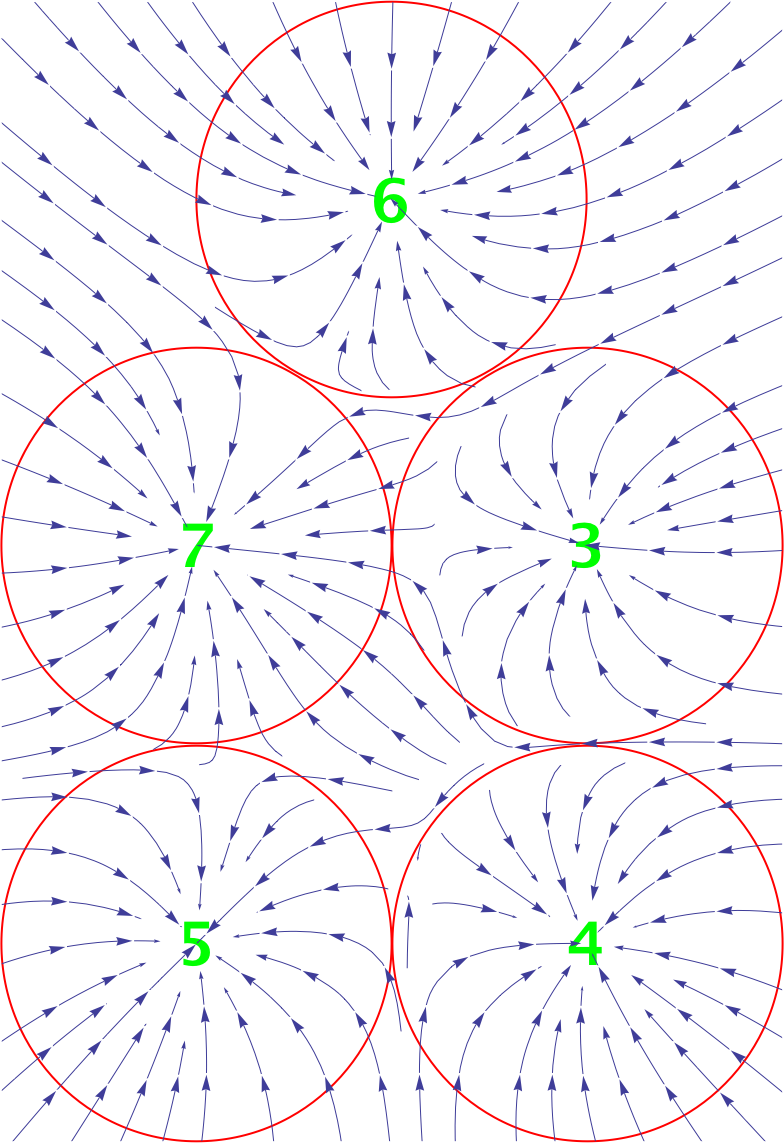
Second (
.nb) has all charges the same, for greater macro symmetry.
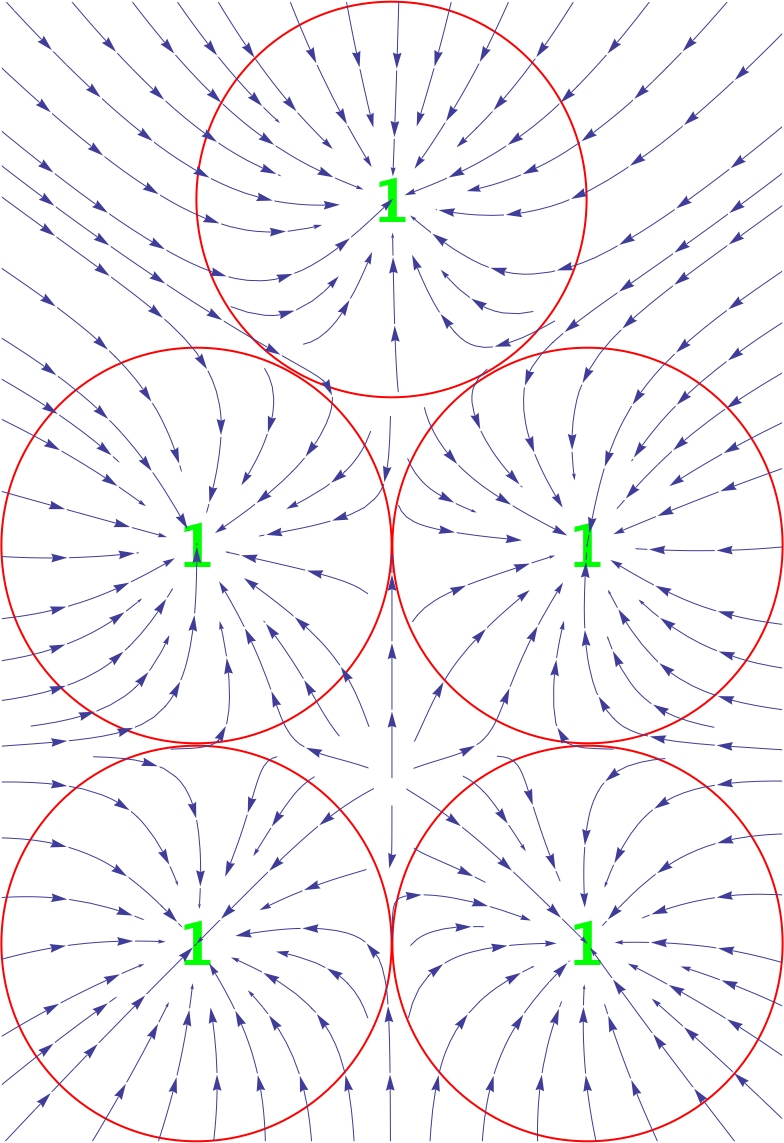
For my taste the variety of charges add to the visual texture, and also reduces the numerical sensitivity near lines of local symmetry.
Re: Software that makes placemats
Posted: 09:13 Sat 29 Jun 2019
by jdaw1
jdaw1 wrote: ↑22:17 Thu 27 Jun 2019{Shudder} Translating that to PostScript would likely as not be 3k lines. {Shudder}
This builds a StreamPlot from a low-resolution two-dimensional array. Ouch. Looking for an algorithm to which takes a function, the function taking (
x,
y) and returning the potential and appropriate derivatives.
Note to self:
Rainer Wegenkittl and Eduard Gröller.
Re: Software that makes placemats
Posted: 11:19 Mon 01 Jul 2019
by akzy
jdaw1 wrote: ↑09:13 Sat 29 Jun 2019
jdaw1 wrote: ↑22:17 Thu 27 Jun 2019{Shudder} Translating that to PostScript would likely as not be 3k lines. {Shudder}
This builds a StreamPlot from a low-resolution two-dimensional array. Ouch. Looking for an algorithm to which takes a function, the function taking (
x,
y) and returning the potential and appropriate derivatives.
Note to self:
Rainer Wegenkittl and Eduard Gröller.
This, I reckon, is going to be significantly harder. I will keep having a look around - there surely is some open source version of it somewhere (haven't had the proper chance to look into the paper you linked yet).
Re: Software that makes placemats
Posted: 19:18 Tue 02 Jul 2019
by jdaw1
This might be easy.
• Don’t have the complicated lines. Instead have separate droplets, starting thin pale grey, ending thicker darker.
• Droplets start on a jittered hexagonal grid. Average distance a parameter, perhaps defaulting to 36pt = ½″ = 12.7mm.
• Droplets advance in small steps downhill (2pt steps?), with no momentum.
• If consecutive steps have angle ≥10°, next step halved. (Or can optimal path length be deduced from second derivatives? Help!)
• Path ends if too close to any charge, or if total distance traversed exceeds some multiple of the average distance apart (perhaps defaulting to 1×).
• That array of path arrays stored, and painted for each page under everything else.
Thoughts?
Re: Software that makes placemats
Posted: 10:00 Wed 03 Jul 2019
by akzy
This seems similar to what I proposed before except we don't do a line fit (as far as I understand) and you start on an arbitrary hexagonal grid. I think the seeds on circle edges might work better, but providing it's easy to play with, have a try both ways.
akzy wrote: ↑17:05 Wed 19 Jun 2019
1. Create field seed spots at the edges of the circles (at whatever density we decide).
2. At that point, we have a vector (from potgridx and potgridy) telling us where the field goes next.
3. Follow that on some small distance (there is definitely a mathematical way of determining how small this distance is - I cant' remember however).
4. Return back to step 2 until you're off the mat or in another circle.
5. Fit a curve to each trace.
Providing your postscript code is fine with calculating potgrid analytically (I have no idea how your conversion tool will deal with the mathematica analytical methods of processing functions) then its just an evaluate, advance, re-evaluate.
jdaw1 wrote: ↑19:18 Tue 02 Jul 2019
• Don’t have the complicated lines. Instead have separate droplets, starting thin pale grey, ending thicker darker.
The darkness of this droplet should be normalised by, for a vector (potgridx and potgridy being the vector in question here) v=(x,y), |v|.
jdaw1 wrote: ↑19:18 Tue 02 Jul 2019
• Droplets advance in small steps downhill (2pt steps?), with no momentum.
• If consecutive steps have angle ≥10°, next step halved. (Or can optimal path length be deduced from second derivatives? Help!)
The size of the step should be normalised by the size of the vector to a first order (i.e.|v|) and the absolute of the first spatial derivative (i.e. |grad(v)|) to a second order. I think for this situation, the latter is the best option. As we already have potgrid calculated analytically, grad(potgrid) can also be calculated analytically, so I believe numerically calculating the second spatial derivative will not be required.
Much easier for me to say this than do it

.
Re: Software that makes placemats
Posted: 06:48 Fri 05 Jul 2019
by jdaw1
akzy wrote: ↑10:00 Wed 03 Jul 2019This seems similar to what I proposed before
Sorry: hapy to acknowledge your prior art, and my slowness of understanding.
akzy wrote: ↑10:00 Wed 03 Jul 2019Providing your postscript code is fine with calculating potgrid analytically
It can.
akzy wrote: ↑10:00 Wed 03 Jul 2019just an evaluate, advance, re-evaluate.
Yes.
akzy wrote: ↑10:00 Wed 03 Jul 2019The darkness of this droplet should be normalised by, for a vector (potgridx and potgridy being the vector in question here) v=(x,y), |v|.
But then it’ll be intense black near charges, and pale grey away. I want a more even grey tone across the page.
akzy wrote: ↑10:00 Wed 03 Jul 2019The size of the step should be normalised by the size of the vector to a first order (i.e.|v|) and the absolute of the first spatial derivative (i.e. |grad(v)|) to a second order. I think for this situation, the latter is the best option.
You’re colouring by intensity of slope — i.e., dark near charges. But I want to choose step size by inverse curvature to lessen the number of “evaluate, advance, re-evaluate” steps. I suspect this will need ∇v.
Re: Software that makes placemats
Posted: 09:39 Fri 05 Jul 2019
by akzy
jdaw1 wrote: ↑06:48 Fri 05 Jul 2019akzy wrote: ↑10:00 Wed 03 Jul 2019
Providing your postscript code is fine with calculating potgrid analytically
It can.
How? More of a curiosity thing than anything. Differentiating analytically using a computer is something I never fully understood (I'm still convinced that wolfram works using magic). If you know of any good explanations (or fancy trying yourself) please send them my way.
jdaw1 wrote: ↑06:48 Fri 05 Jul 2019
akzy wrote: ↑10:00 Wed 03 Jul 2019The darkness of this droplet should be normalised by, for a vector (potgridx and potgridy being the vector in question here) v=(x,y), |v|.
But then it’ll be intense black near charges, and pale grey away. I want a more even grey tone across the page.
My sneaky trick for all of these problems is to whack a logarithm on it somewhere. I had this exact problem trying to produce an electric field graphic for a paper - make the function logarithmic and everything looks better

.
jdaw1 wrote: ↑06:48 Fri 05 Jul 2019
You’re colouring by intensity of slope — i.e., dark near charges. But I want to choose step size by inverse curvature to lessen the number of “evaluate, advance, re-evaluate” steps. I suspect this will need ∇v.
I agree - ∇v is the way to do it. Higher orders wont help. The question is,
what stepsize will it normalise? I think your 2pt idea seems to be a good plan followed by your interpolation of choice.
Re: Software that makes placemats
Posted: 18:56 Fri 05 Jul 2019
by jdaw1
akzy wrote: ↑09:39 Fri 05 Jul 2019∇v is the way to do it.
Let’s say both ∇ and ∇× (grad and curl) are known. What expression is the distance that may be travelled without turning by an angle of more than
a°?
Re: Software that makes placemats
Posted: 20:05 Fri 05 Jul 2019
by akzy
jdaw1 wrote: ↑18:56 Fri 05 Jul 2019
akzy wrote: ↑09:39 Fri 05 Jul 2019∇v is the way to do it.
Let’s say both ∇ and ∇× (grad and curl) are known. What expression is the distance that may be travelled without turning by an angle of more than
a°?
Hmmm. No idea.
However, instead of a angle, you could just set a limit on the absolute value of the curl at that point - effectively the same thing right?
There might be a bit of confusion in the way that I suggested to evaluate so I shall try clarify (if you did understand it, then I've misunderstood something).At a point (x,y), we have a vector, v(x,y) which is pointing in a direction. I suggest that we follow that vector for a step size, h,
h=c / |∇v(x,y)|,
where c is a constant that we chose (be this a few millimeters or whatever works best).
If the field changes a lot in this region, then h will be small, if it changes very little, h will be larger. The vector is then evaluated at v(x+h
x,y+h
y) and the process is repeated.
Re: Software that makes placemats
Posted: 21:45 Fri 05 Jul 2019
by jdaw1
akzy wrote: ↑20:05 Fri 05 Jul 2019h=c / |∇v(x,y)|,
where c is a constant that we chose (be this a few millimeters or whatever works best).
I suspect that curvature, or equivalently ∂angle/∂distance, are related to something like curl÷|grad|². Please help with the specific formal relationship.
Re: Software that makes placemats
Posted: 22:48 Fri 05 Jul 2019
by akzy
The absolute curvature of a field is given by the eigenvectors of the hessian matrix (should give two for our case), where the hessian matrix is

- hessian.PNG (19.79 KiB) Viewed 74881 times
phi_tot is the vector in our case (quick snatch and grab from my thesis)
This eigenvector can be evaluated spatially throughout the field. I suspect you are wanting the angle from the eigenvector. (I found these lecture slides which might help you get what you want, see pages 3 and 4 especially
http://homepages.inf.ed.ac.uk/rbf/CVonl ... ffgeom.pdf)
Re: Software that makes placemats
Posted: 00:23 Sat 06 Jul 2019
by jdaw1
Re: Software that makes placemats
Posted: 08:47 Sat 06 Jul 2019
by akzy
I like it.
I think you will need to make some exceptions for your starting seeds in the gaps between circles to take into account global and local symmetries. Each seed cannot sit on a line of symmetry and must instead sit slightly off (so then it has a definite direction to fly off in, and isn't confused by computational numerical errors).
Re: Software that makes placemats
Posted: 08:53 Sat 06 Jul 2019
by jdaw1
Re: Software that makes placemats
Posted: 08:59 Sat 06 Jul 2019
by jdaw1
akzy wrote: ↑08:47 Sat 06 Jul 2019I think you will need to make some exceptions for your starting seeds in the gaps between circles to take into account global and local symmetries. Each seed cannot sit on a line of symmetry and must instead sit slightly off (so then it has a definite direction to fly off in, and isn't confused by computational numerical errors).
Starting points are a triangular grid, rotated 15°, with moderate random offsets. From these are removed those outside margins. Paths are computed; and then removed are those ending outside the paintable box; and those ending very close to charges.
I think it’s good.
I propose to delete the
Rays feature, which has never worked properly.
Re: Software that makes placemats
Posted: 09:04 Sat 06 Jul 2019
by jdaw1
akzy wrote: ↑09:39 Fri 05 Jul 2019jdaw1 wrote: ↑06:48 Fri 05 Jul 2019akzy wrote: ↑10:00 Wed 03 Jul 2019Providing your postscript code is fine with calculating potgrid analytically
It can.
How? More of a curiosity thing than anything. Differentiating analytically using a computer is something I never fully understood (I'm still convinced that wolfram works using magic). If you know of any good explanations (or fancy trying yourself) please send them my way.
Ahh, misunderstanding. I’ve done the differentiation, and have embedded that as a function which takes the charges and a point
X,
Y. Am not passing around and interpolating inside large 2d arrays of potentials.
Re: Software that makes placemats
Posted: 10:15 Sat 06 Jul 2019
by akzy
This example looks really sharp. I think asymmetric charges will annoy some people to hell, but I think it looks great.
Re: Software that makes placemats
Posted: 22:23 Tue 09 Jul 2019
by jdaw1
I think not. It has curvature in a 3d sense. I want to know how fast the grad turns within the plane.














